4. Begeleiden
4.1 Modelleren en expliciteren
Woorden wekken en voorbeelden trekken
Goede voorbeelden krijgen is een waardevolle manier om iets te leren. Dat is ook zo bij het leren oplossen van problemen. Dit betekent niet dat je, als leerling, een aantal opgeloste problemen voorgeschoteld krijgt. Integendeel, bij een goed voorbeeld zie je hoe iemand een probleem oplost. Het geeft je zicht op hoe het proces verloopt: hoe iemand anders worstelt met een probleem, met inbegrip van het gissen en missen, het uitproberen, het zoeken en het oplossen… We noemen dit modelleren of model staan voor. Daarbij is het nodig dat het zowel voor de leerling als voor de persoon die het probleem oplost over een écht probleem gaat. Anders zie je het zoeken en het worstelen niet.
Deze voorbeeldfunctie met taal ondersteunen, helpt om het leerproces te versterken en te versnellen. We noemen dit ‘je gedachtegang expliciteren’. Je expliciteert op een hoger niveau wat je doet, waarom je dat doet en hoe je dat doet. Als de leraar zelf een heuristiek hanteert, geeft hij die werkwijze ook luidop weer. Leerlingen krijgen zo zicht op wat zich van binnen afspeelt tijdens het oplossen. Dit doen, kost niet veel extra tijd maar vraagt vooral wat aandacht van de leraar. Veel van de stappen die we zetten, zijn immers in ons denken geautomatiseerd. Bijvoorbeeld wanneer we een vraagstukje lezen, noteren we automatisch de gegevens en het gevraagde op een overzichtelijke manier. Dat helpt om het vraagstuk beter te begrijpen. We staan al lang niet meer stil bij wat we doen en waarom we dat doen. Wanneer je expliciteert, breng je dit (opnieuw) onder de aandacht van de leerlingen. We geven drie voorbeelden. Het eerste probleem komt uit een wiskunde-olympiade. We kozen ervoor om dit op te nemen omdat het zo rijk is aan heuristieken. De andere voorbeelden komen uit de dagelijkse wiskundelessen.
Voorbeeld 1: een opgave uit de wiskundeolympiade
Uit Pythagoras (Zoethout, 2017) haalden we de bespreking van deze finalevraag van de Nederlandse wiskundeolympiade van 2016. Het is geschikt materiaal voor een korte ‘workshop over problem solving en bewijzen’ voor leerlingen of (toekomstige) leraren. Het is een klein probleempje dat je op een beperkte tijd kunt behandelen. Doordat er heel wat heuristieken, oplossingsfasen en bewijstechnieken aan bod komen, kun je zichtbaar maken wat er bij een probleemoplosser gebeurt wanneer hij dit probleem oplost. Je kunt het probleem samen met de leerlingen oplossen in een onderwijsleergesprek waarbij je expliciet aandacht besteedt aan het verwoorden van de heuristieken en bewijstechnieken (zie de tussentiteltjes in de uitwerking hieronder). Ook de fasen van het oplossingsproces maak je hierbij zichtbaar (we bespreken dit op het einde). Het probleem is, ondanks de inkleding, zuiver wiskundig.
Het lezen van een uitgeschreven oplossing is vooral interessant voor wie vooraf over het probleem heeft nagedacht. We raden de lezer dan ook aan om eerst zelf na te denken over de oplossing.
Heuristieken en bewijstechnieken expliciteren
Opgave
Op een lange stoep staat een rij van getallen geschreven met stoepkrijt. De getallen hoeven niet op volgorde van klein naar groot te staan en ze hoeven niet allemaal verschillend te zijn. Merlijn omcirkelt van de getallen met rood krijt. De rood omcirkelde getallen blijken van links naar rechts precies de getallen te zijn. Vervolgens omcirkelt Jeroen van de getallen met blauw krijt. De blauw omcirkelde getallen blijken van links naar rechts precies de getallen te zijn. Bewijs dat het middelste getal in de rij van getallen zowel rood als blauw omcirkeld is.
Heuristieken: verband zoeken tussen de gegevens, werken met kleinere aantallen
De getallen 999 en 500 zijn te groot om het probleem eventjes (bv. op een blad papier bij gebrek aan een stoep en stoepkrijt) te visualiseren. Een eerste heuristiek die we kunnen toepassen is werken met kleinere aantallen, zodat het probleem overzichtelijker wordt. De aantallen 999 en 500 zijn op zich niet essentieel, maar het zijn ook niet zomaar twee getallen. Ze zijn verbonden door het verband: . Ervan uitgaande dat dit verband belangrijk is, kunnen we bv. beginnen met 5 getallen waarvan er 3 in het rood en 3 in het blauw omcirkeld worden (immers ). Het eenvoudiger probleem met kleinere getallen luidt dan:
Op de stoep staat een rij van vijf getallen, Merlijn omcirkelt er drie in het rood en deze blijken van links naar rechts te zijn. Jeroen omcirkelt er drie in het blauw en dit blijken van links naar rechts te zijn. Bewijs dat het middelste getal twee keer omcirkeld is.
Heuristieken: voorbeelden bekijken, eigenschappen vaststellen
We bedenken enkele voorbeelden die voldoen aan de voorwaarden van het probleem met vijf getallen.

We zien op de voorbeelden dat het middelste getal inderdaad telkens twee keer omcirkeld is. Deze vaststelling is natuurlijk nog geen bewijs! Maar op de voorbeelden kun je nog meer vaststellen: het middelste getal is het enige dat dubbel omcirkeld is. Kunnen we alvast bewijzen dat er altijd juist één getal is dat dubbel omcirkeld is? Misschien is dat nuttig en kunnen we daarna bewijzen dat dit het middelste getal is.
Heuristiek/bewijstechniek: opdelen in deelproblemen
Om te bewijzen dat er juist één getal is dat dubbel omcirkeld is, gaan we achtereenvolgens bewijzen dat er minstens één dubbel omcirkeld getal is en dat er niet meer dan één dubbel omcirkeld getal is.
Bewijstechniek: het duivenhokprincipe
Zoals aangekondigd bewijzen we eerst dat er minstens één dubbel omcirkeld getal is. Omdat er zes cirkels getekend zijn en er maar vijf getallen zijn, moet er minstens één getal zijn dat dubbel omcirkeld is. Dit is het duivenhokprincipe: als er meer duiven zijn dan hokjes, is er minstens één hokje met minstens twee duiven. De duiven zijn hier de cirkels, de hokjes de getallen.
Dezelfde duivenhokredenering werkt ook met de grotere aantallen: Merlijn en Jeroen tekenen in totaal 1000 cirkels rond 999 getallen, dus minstens één getal is dubbel omcirkeld.
Bewijstechniek: bewijs uit het ongerijmde
Heuristieken: terugdenken aan eerdere bewijzen; getallen voorstellen door letters; een veronderstelling maken die geen afbreuk doet aan de algemeenheid
We bewijzen nu dat er niet meer dan één dubbel omcirkeld getal is. Dit is typisch een uitspraak om uit het ongerijmde te bewijzen. Of leerlingen hieraan denken, hangt af van hun wiskundige voorgeschiedenis: hebben ze al eerder een gelijkaardige uitspraak uit het ongerijmde bewezen? In dat geval kun je ook zeggen dat hier de heuristiek gebruikt wordt: terugdenken aan eerdere problemen of bewijzen.
Veronderstel dat er minstens twee getallen zijn die dubbel omcirkeld zijn. Noem die getallen en en veronderstel dat links van staat (niet noodzakelijk als directe buren). Nu zijn en allebei zowel in het rood als in het blauw omcirkeld. Omdat en rood omcirkeld zijn, geldt . Omdat en blauw omcirkeld zijn, geldt . Dit geeft een tegenspraak. De veronderstelling dat er minstens twee dubbel omcirkelde getallen zijn, is dus niet houdbaar. Merk op dat deze redenering evengoed werkt voor 999 getallen als voor 5 getallen.
Heuristiek: een tussentijdse stand van zaken opmaken
Tot nu toe hebben we bewezen dat precies één getal dubbel omcirkeld is. Nu moeten we nog aantonen dat dit het middelste getal is.
Heuristiek: de concrete voorbeelden bekijken, eigenschappen vaststellen
Bewijstechniek: bewijs uit het ongerijmde
In de voorbeelden van vijf getallen stellen we ook vast dat er geen niet-omcirkelde getallen zijn. Ook dit bewijzen we uit het ongerijmde. We doen dit meteen voor de rij van 999 getallen. Stel dat er een getal is van die 999 dat niet omcirkeld is, dan zijn er maar 998 getallen die omcirkeld zijn met 1000 cirkels. Omdat geen enkel getal drie keer of meer omcirkeld is, volgt hieruit dat er twee getallen zijn die dubbel omcirkeld zijn. Maar we hebben zonet bewezen dat dit onmogelijk is. Dus: alle getallen zijn omcirkeld.
Heuristiek: de concrete voorbeelden bekijken, eigenschappen vaststellen
We kijken in de voorbeelden met vijf getallen naar de getallen links van het dubbel omcirkelde getal. We stellen vast: de getallen kleiner dan het dubbel omcirkelde getal komen hier elk juist één keer voor en zijn rood omcirkeld. De getallen groter dan het dubbel omcirkelde getal komen hier ook elk juist één keer voor en zijn blauw omcirkeld.
Heuristieken: getallen voorstellen door letters, rekenen met letters
Laten we deze eigenschap bewijzen voor de 999 getallen. Noem het dubbel omcirkelde getal . De getallen links van zijn allemaal één keer omcirkeld. De getallen links van die in het rood omcirkeld zijn, moeten zijn. Dit zijn er dus . De getallen links van die in het blauw omcirkeld zijn, moeten zijn. Dit zijn er . In totaal zijn er dus getallen links van .
Heuristiek: beseffen dat het probleem opgelost is
Als er 499 getallen links van staan, van de 999, dan is het 500ste getal in de rij en zijn er ook rechts van 499 getallen. Dit betekent dat inderdaad het middelste getal is!
Fasen van het oplossingsplan
Niet enkel bewijstechnieken en heuristieken, maar ook fasen van het oplossingsproces zijn hier mooi in terug te vinden. De stukjes horende bij de eerste twee tussentitels verwijzen naar het analyseren van het probleem: wat is het, begrijp ik goed wat de vraag is, zijn de getallen willekeurig, krijg ik greep op wat erachter zit…? Dan wordt een plan opgesteld: de beslissing om alvast te bewijzen dat er altijd juist één getal is dat dubbel omcirkeld is. Dit plan wordt dan uitgevoerd. De cyclus van analyseren, plannen en uitwerken wordt nog twee keer toegepast: eerst over het feit dat alle getallen omcirkeld zijn en dan over de getallen links van het dubbel omcirkelde getal. Op het einde is er een fase van reflectie. Is alles wel bewezen? Is mijn bewijs onafhankelijk van de gekozen voorbeelden? Is het algemeen genoeg?
Voorbeeld 2: het angula-probleem
De voorgaande opdracht was een speciale opdracht waarmee je typische heuristieken en bewijstechnieken kunt illustreren. Om problemen te leren oplossen, is het nodig om vaak genoeg deze duiding bij voorbeelden te geven en daarvan ‘een zaak van elke dag’ te maken. Je hoeft daarvoor geen speciale opgaven te zoeken. Integendeel, de meeste opgaven die je oplost vormen in het begin ‘een probleem’ voor de leerlingen. Het expliciteren van hoe je het aanpakt en waarom je dat zo doet, kun je moeiteloos in je gewone onderwijsleergesprekken verwerken. Voor het tweede voorbeeld grijpen we terug naar het angula-probleem van de tweede paragraaf.
Het zoeken zichtbaar maken
Opgave
Los het volgende Indische rekenprobleempje (ongeveer 840 na Chr.) op. Een heel bijzondere slang van angula’s lang kruipt in \frac{5}{14} van een dag 7,5 angula’s diep in een hol. In \frac{1}{4} van een dag groeit ze echter \frac{11}{4} van een angula aan. Hoelang zal het duren tot ze volledig in het hol verdwenen is?
Ordenen en herformuleren van de gegevens en het gevraagde
Ik maak graag een overzicht van wat we weten en wat we zoeken. Wanneer ik straks een gegeven zoek, kan ik dat snel terugvinden.
Gegeven
- Lengte slang: 80 angula’s
- Kruiptijd: \frac{5}{14} dag Kruiplengte: 7,5 angula = \frac{15}{2}angula
- Groeitijd: \frac{1}{4} dag Groeilengte: \frac{11}{4} angula
Gevraagd: Hoelang duurt het voor ze volledig in het hol verdwenen is?
Vereenvoudigen van de gegevens
De gegevens bevatten twee verbanden tussen afstand (lengte) en tijd. De tijden verschillen waardoor je deze gegevens maar moeilijk kunt combineren. De grootheden afstand en tijd zijn hier evenredig waardoor we ze kunnen herleiden naar gelijke tijden. Ik gebruik een verhoudingstabel en vermenigvuldig in de ene met \frac{14}{5} en de andere met 4. Een onverwachts voordeel is dat de breuken verdwijnen.
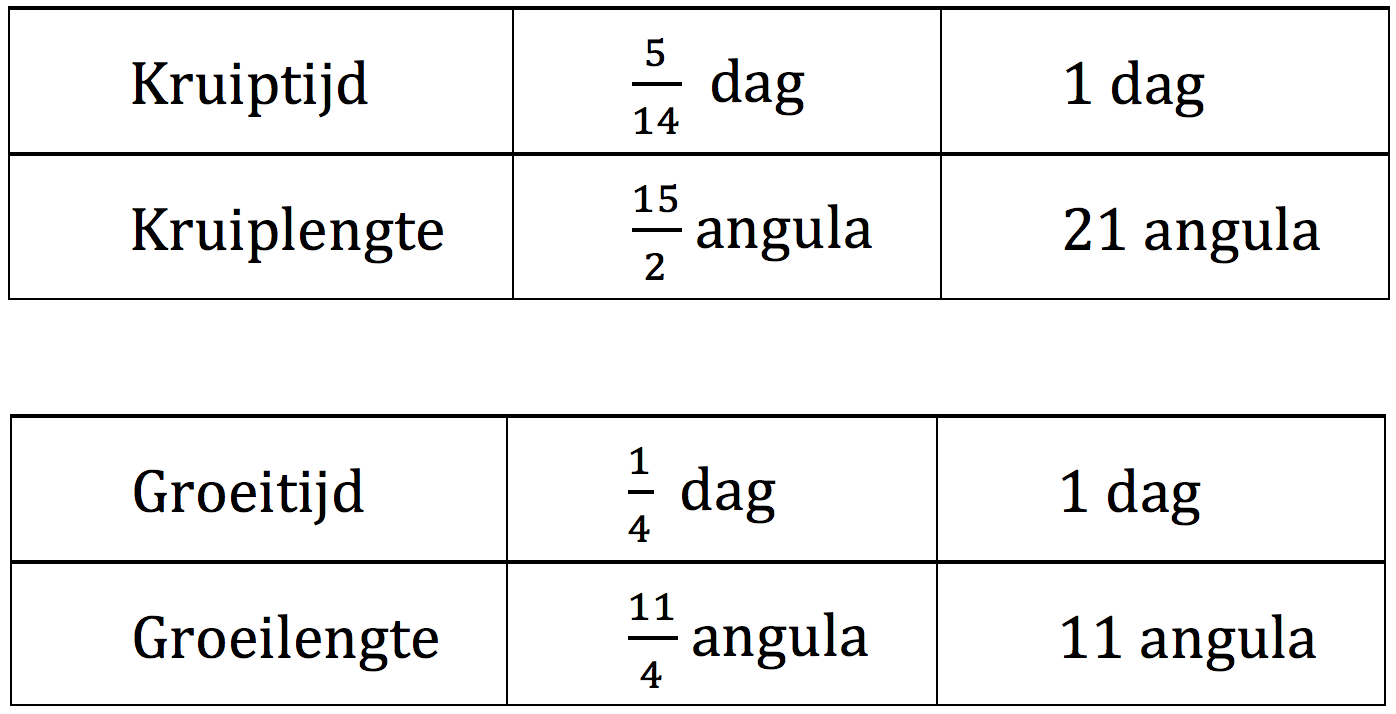
Een schets maken om het probleem beter te begrijpen
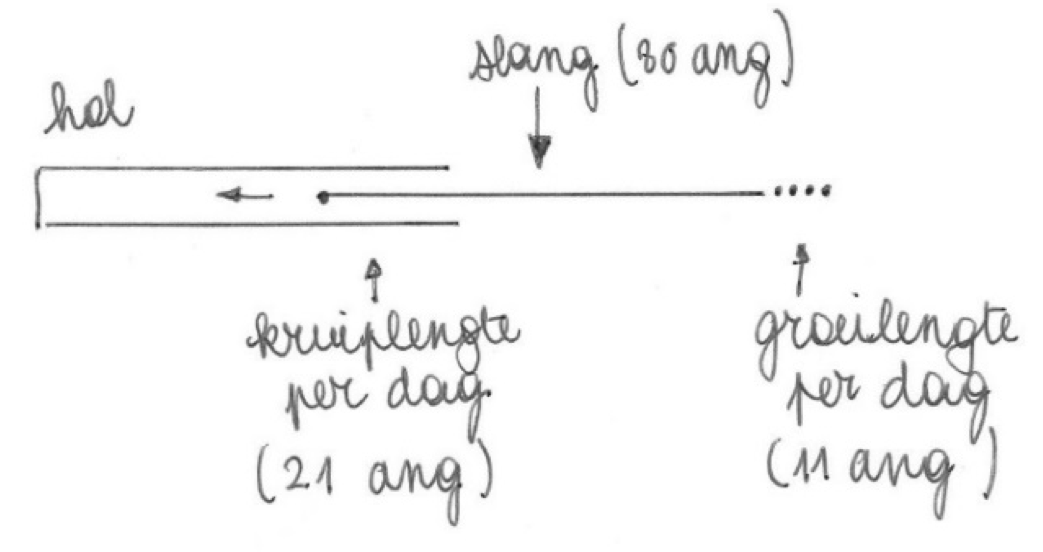
Ik zie op de schets dat de slang sneller, bijna dubbel zo snel, in het hol kruipt dan dat ze groeit. Ze zal dus helemaal in het hol verdwijnen.
Uitproberen door te gissen en te missen
Ik probeer het probleem nog beter te begrijpen. Per dag kruipt de slang 21 angula’s in het hol. Er komt dus elke dag een lengte van 21 angula’s in het hol bij. Per dag groeit de slang 11 angula’s. Er komt dus elke dag 11 angula’s bij de lengte van de slang bij. Ik zet dit in een tabel voor wat overzicht. Ik ben me er van bewust dat dit geen verhoudingstabel is.

Ik zoek wanneer de lengte in het hol gelijk is aan de lengte van de slang. Ik merk op dat dit niet op een geheel aantal dagen uitkomt. Ik heb een andere aanpak nodig.
Vertalen van de verbanden naar wiskundetaal
Ik moet het moment vinden waarop
lengte slang = lengte in het hol
Ik zoek hoe ik deze lengtes kan beschrijven in functie van de tijd (in dagen). Uit de bovenstaande tabel haal ik de verbanden:
\begin{align*}11\cdot t + 80 &= 21\cdot t\\ 80 &= t(21-11)\\ t &= \frac{80}{10}=8\end{align*}
Na 8 dagen is de slang helemaal in het hol verdwenen. Hé, dat is een geheel getal?
Controleren van de oplossing
Ik herbekijk de tabel en merk dat ik in de onderste rij een rekenfout gemaakt heb. 144 moet 146 zijn en dan zijn de daaropvolgende getallen ook fout. Het maakt zichtbaar hoe noodzakelijk het is om een oplossing te controleren. Door het antwoord op twee verschillende manieren te vinden, kan ik gemakkelijk de fout herkennen.
Voorbeeld 3: een goniometrische identiteit
In heel veel richtingen staat goniometrie op het leerplan. Ik (Gerd) sta zelf in het vijfde jaar tso, 4 uur wiskunde per week. Goniometrie staat ook al in het derde en vierde jaar op het leerplan. In het vijfde jaar komt heel wat van de leerstof terug in het kader van goniometrische functies. Heel veel leerlingen hebben het moeilijk om identiteiten te bewijzen en om goniometrische formules te vereenvoudigen (met som- en verschilformules, formules van Simpson…). Sommige leerlingen hebben hier zicht op, andere totaal niet en berusten in het feit dat ze dat niet kunnen. Ik heb ook dikwijls het gevoel dat te veel leerlingen niet groeien in dit onderwerp.
Ik ben op zoek gegaan naar wat ze kan helpen.
Ik vergelijk het met een bouwvakker. Hij of zij heeft meestal een gereedschapskist bij zich en moet goed weten welk materiaal er in zijn kist zit, waarvoor het dient en hoe hij het moet gebruiken. Naarmate de jaren vorderen heeft hij meer en dikwijls specifieker gerei voor een bepaalde taak. Als hij een probleem moet oplossen, moet hij eerst ter plekke gaan kijken, het probleem analyseren, beslissen welk materiaal hij zal inzetten om het probleem op te lossen. Soms zijn er meerdere interventies nodig. Gezond verstand is ook altijd meegenomen! Tenslotte is het raadzaam dat zijn probleem niet ingewikkelder wordt na een interventie!
Voor wiskunde wordt de gereedschapskoffer naarmate de jaren vorderen ook meer gevuld en wordt er verder gebouwd op kennis en kunde uit de vorige jaren. Het is goed af en toe stil te staan bij wat er allemaal al in de wiskundekoffer zit en ook voldoende tijd te steken in het herhalen en terug paraat maken van de kennis die de revue al passeerde en waar we vanuit gaan dat leerlingen deze kunnen gebruiken.
Om identiteiten bij goniometrie te bewijzen, kun je je afvragen wat er allemaal voorhanden is.
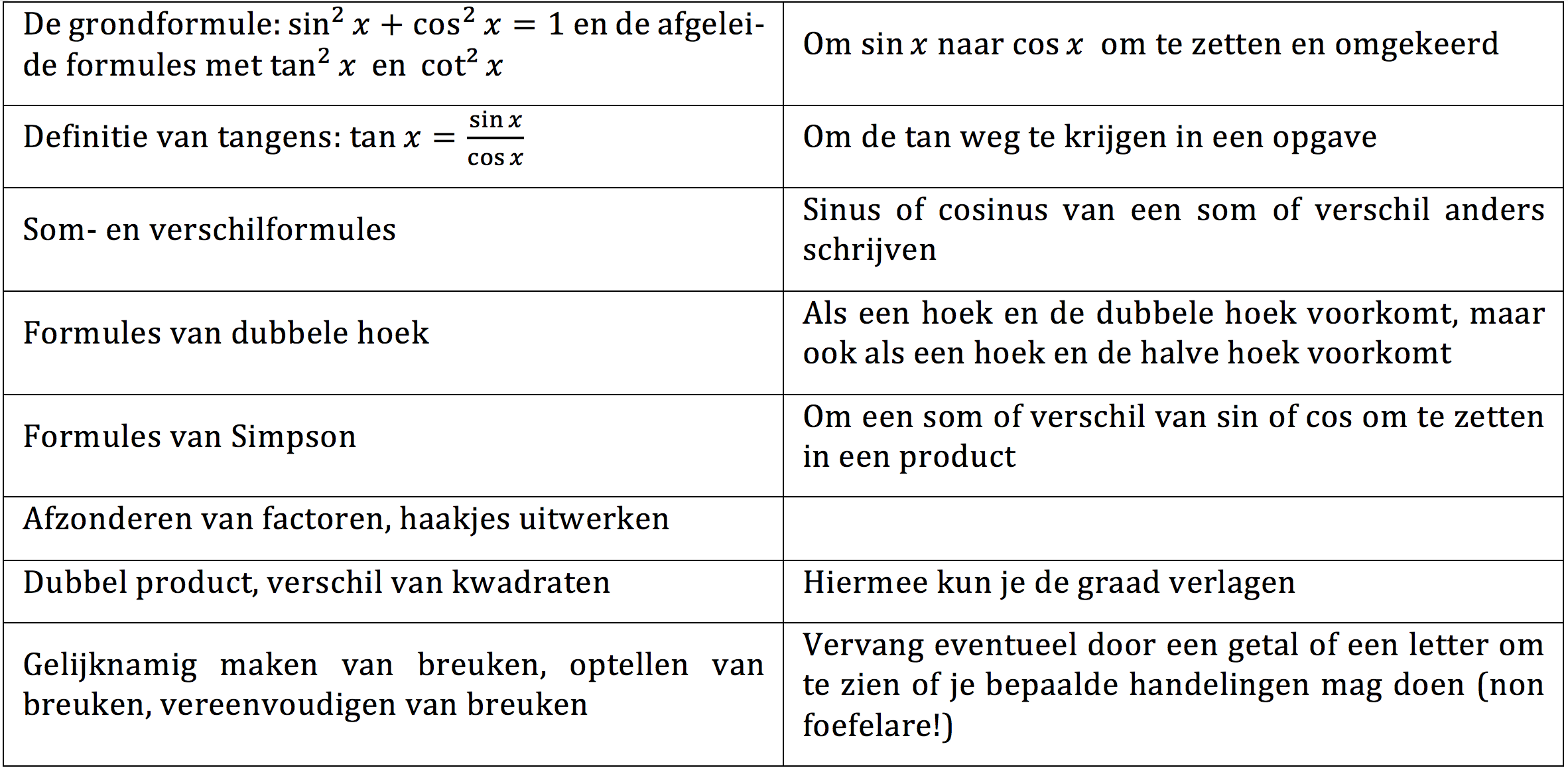

Deze lijst is zeker niet volledig. Je hebt nog verbanden van hoeken in een driehoek, formules voor verwante hoeken… Soms haal je een truc van de foor uit: een hoek delen door 2 en vermenigvuldigen met 2, schrijven als , … Het is daarbij heel belangrijk te laten zien waarom je deze truc uithaalt: om een formule van halve hoek te kunnen gebruiken, omdat er niets anders kan…
Nog enkele tips die je de leerlingen kunt meegeven:
- Laat de oefening spreken, heel dikwijls kun je niet anders dan één bepaalde techniek toepassen.
- Soms is het goed om het linkerlid om te vormen tot je het rechterlid krijgt, soms is het beter te beginnen met het rechterlid en soms is het beter linker- en rechterlid tegelijkertijd om te vormen tot je hetzelfde krijgt.
- Probeer te voorzien wat er gaat gebeuren voor je iets doet: bepaalde factoren zullen kunnen geschrapt worden; de grondformule komt tevoorschijn; wordt het niet ingewikkelder (bv. hogere graad, vierkantswortel…)?
- Je moet op tijd controleren of je oplossingsmethode goed is: gaat dit de goede richting uit of wordt het alleen maar ingewikkelder? Zou de leraar dit nog willen nakijken? Soms verdienen leerlingen een medaille voor doorzettingsvermogen maar zouden ze beter stoppen en nadenken over een andere methode!
Enkele tips voor de leraar:
- Laat ook aan het bord zien dat niet alles lukt wat je probeert.
- Laat leerlingen met verschillende oplossingsmethodes aan bord komen en uitleggen wat ze gedaan hebben en waarom.
- Laat leerlingen eerst samenwerken in groepjes van twee, dan in groepjes van vier. Zo geraken ze meestal verder, vooral in het verduidelijken van waarom ze een bepaalde stap zetten.
- Laat leerlingen zoeken op allerlei mogelijkheden om met een bepaalde oefening te starten. Pas daarna bespreek je met welke start je het verst geraakt in de richting van wat je moet bewijzen.
Om bijvoorbeeld aan te tonen dat \cos 3x = 4cos^3 x – 3\cos x, kun je in het linkerlid enkel 3x schrijven als som van 2x en x. In het rechterlid kun je \cos x afzonderen.
Het is belangrijk om voorbeelden en oefeningen goed te kiezen. Om succeservaring te creëren moeten leerlingen door aangeleerde technieken ook de volgende oefeningen kunnen maken. In een huiswerk of test een oefening aanbieden waar ‘weer iets anders uit de wiskundige gereedschapskoffer’ moet gehaald worden dat niet herhaald is, is geen goed idee. Je kunt dit natuurlijk wel aanbieden als ‘nieuw probleem’ omdat het peilt naar het kunnen vinden van de juiste wiskundekennis.
We geven nog een uitgewerkt voorbeeld waarbij we telkens duidelijk maken wat we doen en waarom.
Een goniometrische identiteit
Bewijs van een driehoek dat
\sin \alpha + \sin \beta + \sin \gamma = 4\cos\frac{\alpha}{2}\cdot\cos\frac{\beta}{2}\cdot\cos\frac{\gamma}{2}.

4.2 Metacognitieve vaardigheden ontwikkelen
Zoals je in de vorige paragraaf kon lezen, is het opnemen van een voorbeeldfunctie en die expliciteren een eerste manier om leerlingen te leren om problemen op te lossen. Je kunt dat vergelijken met een skileraar die voordoet hoe je goed de berg af skiet en uitlegt hoe je dat moet doen en waarom dat werkt.
Maar er is meer nodig. Naast inzicht krijgen in hoe een oplossingsproces verloopt en wat ze daarbij kunnen inzetten, moeten leerlingen zichzelf kunnen sturen tijdens dit proces. We noemen dit metacognitieve vaardigheden ontwikkelen. Jezelf leren sturen betekent ‘niet langer iemand nadoen’ maar ‘het denkwerk zelf doen’. Naarmate het leerproces verder loopt, neemt de leraar minder een voorbeeldfunctie op en zet hij meer in op begeleiding die de zelfstandigheid en zelfsturing ontwikkelt. Dit wil zeggen dat een leraar het denken zoveel mogelijk bij de leerling legt en zelf zo weinig mogelijk voordoet. Hij beperkt de informatie die hij geeft tot een minimum. Net genoeg opdat de leerling de volgende stap zelf kan bedenken.
Dat geeft aanleiding tot vragen als ‘heb je het vraagstuk goed gelezen?’, ‘weet je wat je moet doen?’, ‘is er al iets dat je weet over de oplossing?’, ‘hoe kun je hier aan beginnen?’…
Voor leraren is dat gewoonlijk niet gemakkelijk. We zijn er immers op gericht om leerlingen verder te helpen, om hen hulp te bieden om de oplossing te vinden en te begrijpen. Informatie (nog) achterhouden past daar op het eerste gezicht niet in. Zeggen hoe het moet of hoe het in elkaar zit, is in dit geval niet ondersteunend. Integendeel, dit soort hulp neemt net het denken bij de leerlingen weg.
Een tweede factor die het moeilijk maakt, is het tijdverlies. Oplossingsgericht verder helpen, is immers veel sneller en veel efficiënter. Je denkt gemakkelijk ‘ik zal het snel even uitleggen of voordoen’. Metacognitieve vaardigheden ontwikkelen vraagt constant afweging wat op het gegeven moment primeert. Laat ik hier de leerling het denkwerk doen zodat hij bijleert hoe je dit soort dingen aanpakt? Of doe ik nu het denkwerk omdat vooruitgang op dit moment belangrijker is? In het volgende stukje beschrijven we een hulpmiddel dat kan helpen om zicht te krijgen op interventies. We geven twee voorbeelden ter illustratie.
Een kader om gericht te interveniëren
We onderscheiden drie niveaus waarop je hulp biedt. Hoe hoger het niveau is waarop je hulp biedt, hoe minder specifiek die zal zijn en hoe meer het denken bij de leerlingen ligt.
De drie grote categorieën van interventies zijn:
- hulp die erop gericht is om het probleem te verduidelijken,
- hulp die erop gericht is om een oplossing te vinden,
- helpen oplossen.
Bij de verschillende categorieën kun je nog verder onderscheid maken. Dat zie je in het onderstaande overzicht. Niet alle stapjes die we beschrijven, kun je op elk moment of bij elk probleem toepassen.

Een onvolledige vergelijking van de tweede graad
Opgave
Los de volgende vergelijking op:
2x^2-3x=0.
Het is al enige tijd geleden dat de leerlingen tweedegraadsvergelijkingen hebben leren oplossen. Deze vergelijking was een deelopdracht bij een ruimere opdracht. Vaak zie ik leerlingen vervallen in het (fout) oplossen van deze vergelijking met behulp van een discriminant.
- De probleemsituatie beschrijven: ‘we hebben een vergelijking die we moeten oplossen’.
- De probleemsituatie verhelderen: ‘we zoeken waarden voor x. Als we die invullen op de plaats van x, dan klopt de gelijkheid’ of ‘het is een onvolledige vergelijking’.
- Uitnodigen om gericht te denken: ‘wat voor soort vergelijking is dit?’, ‘op welke manier kunnen we die oplossen?’, ‘heb je al iets geleerd dat je hierbij zou kunnen gebruiken?’, ‘Waarom past deze opgave in dit hoofdstuk?’.
- Nog te onderzoeken oplossingsmethode aangeven: ‘is er een algemene methode?’ of ‘is er misschien een kortere methode?’
- Meerdere juiste oplossingsmethodes aangeven: ‘je kunt werken met de discriminant of je kunt ontbinden in factoren’.
- Eén juiste methode aangeven: ‘ontbinden in factoren’.
- Uitleggen hoe het moet: ‘je brengt x buiten haakjes en dan kijk je wanneer een factor nul wordt’.
- Voordoen: ‘als ik x^2+3x=0oplos, dan breng ik x buiten haakjes. Dan krijg ik x(x+3)=0. Een product wordt 0 als één van de factoren 0 is. Dit betekent als x=0 of x=-3. Hoe ziet dat er bij jouw voorbeeld uit?’.
- Samen doen: ‘we zetten de gemeenschappelijke factor voorop. We krijgen een tweede factor 2x-3. Het product wordt 0 als x=0 of x=\frac{3}{2} ’.
- In de plaats van de ander doen: ‘even de balpen van de leerling nemen en een stapje schrijven om het vooruit te laten gaan’.
Het is natuurlijk niet de bedoeling om de verschillende stapjes systematisch te doorlopen. Het kader is een middel om je stil te laten staan bij het soort hulp dat je geeft. In het volgende voorbeeld gaan we soepeler met het model om en zoeken we welke hulp we kunnen bieden binnen de grote categorieën.
Irrationale functies
Opgave
Zijn de volgende twee functies dezelfde?
f(x)=\sqrt{(x-1)(x+2)} en g(x)=\sqrt{x-1}\cdot\sqrt{x+2}
Een gelijkaardige vraag zou kunnen zijn:
Hebben de volgende vergelijkingen dezelfde oplossingen?
\sqrt{(x+2)(x-3)}=6 en \sqrt{x+2}\cdot\sqrt{x-3}=6
Bij de oplossing probeer je het denken zoveel mogelijk bij de leerlingen te leggen door vragen te stellen die zo weinig mogelijk informatie geven. Bedenk zo veel mogelijk interventies die je zou kunnen doen die de leerlingen verder kunnen helpen bij het oplossen van deze opgave.
Interventies gericht op zelfsturing om de oplossing vinden
- Hoe kunnen we aan dit probleem beginnen?
- Wat zijn de verschillen tussen de twee functies?
- Wat staat er in je boek of nota’s dat je kunt gebruiken om dit probleem op te lossen?
- Wat weten we en wat zoeken we?
- Waarom zou deze opgave bij dit hoofdstuk staan?
- Zou je kunnen denken dat de twee functies hetzelfde zijn?
- Lijken deze functies op elkaar? Waarin verschillen ze? Waarin zijn ze hetzelfde?
- Wat is er belangrijk bij irrationale functies? Wat is er anders dan bij veeltermfuncties of rationale functies?
- Wat zijn elementen die helpen bij het onderzoeken van functies?
Interventies gericht op het oplossen
- Waarom zou je kunnen denken dat het twee dezelfde functies zijn?
- Wat kunnen we allemaal onderzoeken wanneer we een irrationale functie bestuderen? Domein, beeld, nulwaarden, tekenverloop, grafische voorstelling…
- Onderzoek eens het domein van beide functies.
- Bepaal het domein van , bepaal het domein van en vergelijk beide domeinen met elkaar.
- Wanneer bestaat een wortel van een getal?
- Kun je dat eens met getallen noteren? Voor welke getallen gaat dat, voor welke niet?
- …
In deze context wordt er vaak gesproken over de leraar als coach. Dat klopt wel. Toch houdt het ook risico’s in om dat zo te benoemen. Wanneer je jezelf observeert bij het stellen van vragen die van hoog niveau zijn en dus weinig informatie bevatten, lijken dat vooral algemene en vage vragen te zijn: hoe begin je hieraan, wat weet je al, is er iets dat je herkent… Als je de vragen hoort, krijg je de indruk dat er weinig wiskundige expertise nodig is en dat iedereen deze rol wel kan opnemen. Nochtans heb je net veel vakkennis nodig om de juiste vragen te kunnen stellen. Enerzijds moet je inzicht hebben in een goede oplossing van het probleem en anderzijds in de metacognitieve processen om het probleem op te lossen. Daarbovenop is het nodig om goed het perspectief van de leerling te kunnen innemen. Dan kun je net die interventie doen waarmee je zo weinig mogelijk informatie aan de leerling geeft zodat die toch de volgende stap kan zetten om het probleem op te lossen.
Het is ook goed om een zekere systematiek te steken in je interventies, bijvoorbeeld door steeds dezelfde vragen te stellen: ‘kijk eerst goed naar de opgave’, ‘zoek eens een patroon’, ‘waarom staat deze opgave bij dit hoofdstuk?’…
Tot slot is het goed om te beseffen dat er grenzen zijn aan de begeleiding die je als leraar kunt bieden. Een goede voorbeeldfunctie opnemen waarbij je expliciteert wat je doet en waarom je dit doet en inzet op groeiende zelfsturing en zelfstandigheid betekent al heel wat. Lukt het daarmee nog niet, dan is mogelijk iets anders nodig, bijvoorbeeld heroriëntering.



 Onder de loep
Onder de loep



