5.2 Veiligheid bieden
Je eigen houding ten opzichte van problemen
Problemen oplossen is een proces waarbij heel wat emoties naar boven komen, zelfs bij leerlingen die fan van wiskunde zijn en dit goed kunnen. In de onderstaande figuur zie je hoe tijdens het maken van een opgave de emoties wisselden bij een nochtans enthousiaste leerling (Op ’t Einde, 2006). De leerling loste een opgave op die bestond uit een aantal deelopgaven. De leerling kreeg eerst een oriëntatie op de opdracht en ging dan aan het werk. Op een bepaald moment ging de bel (ring!!) wat het sein was dat de tijd bijna op was. Zijn emoties tijdens het oplossen varieerden van blijdschap, trots, geluk en opluchting tot bezorgdheid, paniek, frustratie, woede en stress (figuur 1).
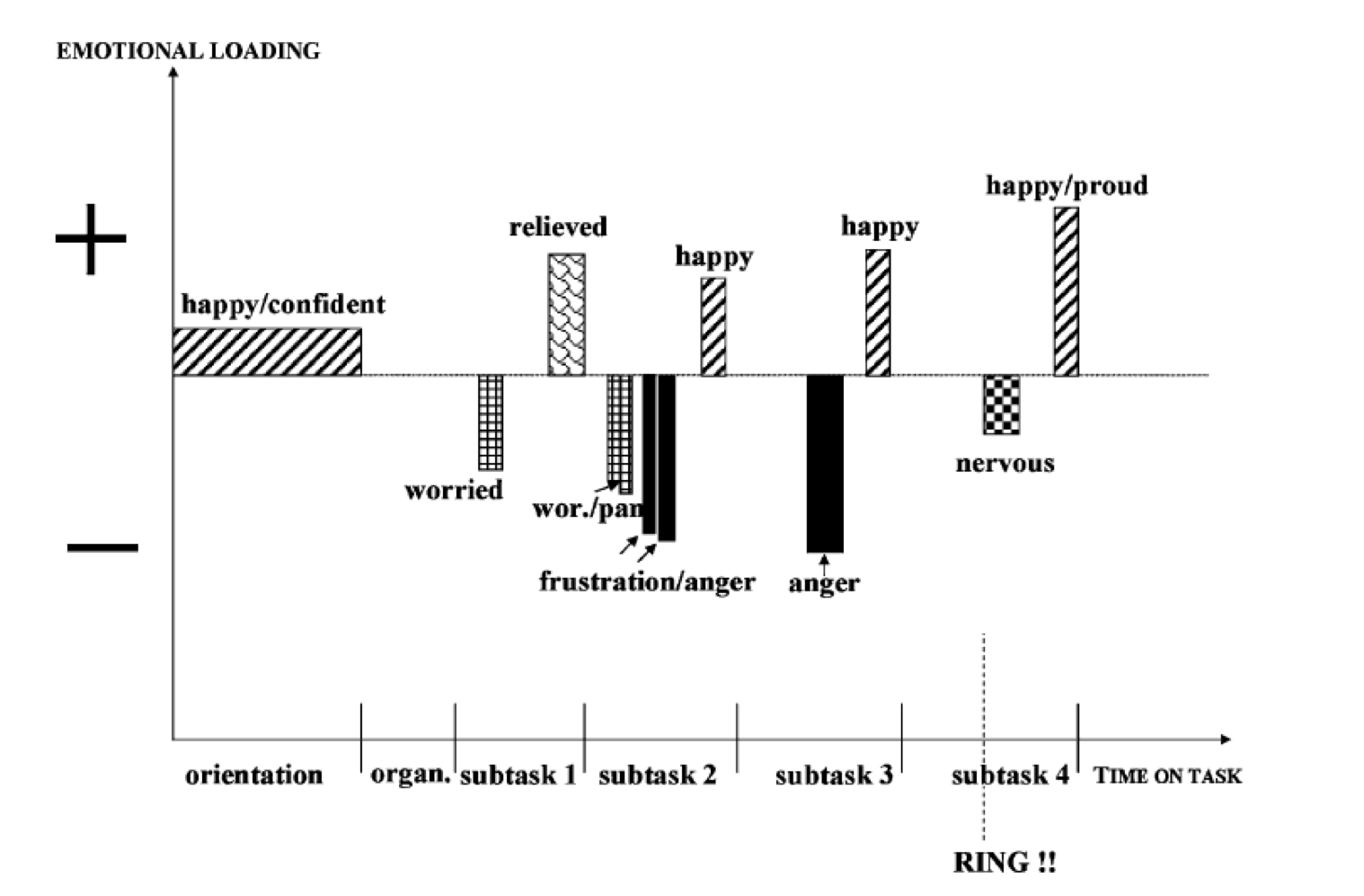
Figuur 1
Sommige mensen genieten van een onopgelost probleem. Ze vinden het een uitdaging en zoeken die problemen op. Ze kunnen blijkbaar goed om met deze wisselende emoties en het ongemak dat dit met zich mee brengt. Ze hebben een hoge ‘ongemaksdulding’ (Bos, 2015). Anderen hebben het hier erg moeilijk mee. Ze houden absoluut niet van onopgeloste problemen en willen die liefst zo snel mogelijk opgelost zien of gaan ze uit de weg. Deze mensen hebben een lage(ere) ongemaksdulding. Ze kunnen maar moeilijk om met het gevoel van onzekerheid. Je weet immers nooit op voorhand óf je dit probleem zult kunnen oplossen (anders is het geen echt probleem) en óf de oplossing je zal bevallen. Vaak uit zich dat ook in ‘niet willen beginnen’ of ‘snel opgeven’. Wanneer we leerlingen leren om problemen op te lossen, is het leren omgaan met dit ongemakkelijk gevoel of je ongemaksdulding verhogen een element in het leerproces.
Hoe je als leraar zelf ten opzichte van problemen staat en hoe je ze ervaart, speelt hierbij een rol. Wanneer je zelf moeite hebt met het toelaten van dit ongemak, is het heel moeilijk om leerlingen te leren hiermee om te gaan. In dat opzicht is het interessant om je eigen klaspraktijk te onderzoeken. Ben je eerder een leraar die ervoor zorgt dat leerlingen zo weinig mogelijk problemen tegenkomen. Of zorg je er net voor dat het fout loopt en dat er problemen op tafel komen te liggen? We geven een voorbeeld over het optellen en aftrekken van ongelijknamige breuken maar ook hier kan je dit gemakkelijk vertalen naar andere klassituaties.
Optellen en aftrekken van ongelijknamige breuken
Bij het optellen en aftrekken van ongelijknamige breuken is het nuttig om voorbeelden te geven waarmee je de bewerkingen in de realiteit plaatst. Dit helpt leerlingen om de bewerking beter te begrijpen en ze later in vraagstukken te herkennen.
Een situatie zoeken die aanleiding geeft tot het optellen van breuken is eenvoudig. Bv. \frac{1}{2}+\frac{1}{4}
‘Ik eet eerst een halve appel en daarna nog een kwart appel. Welk deel van de appel heb ik gegeten?’
Het goed formuleren van een situatie voor de aftrekking van twee breuken bevat meer hindernissen.
Bij de bewerking \frac{1}{3}-\frac{1}{5} komt waarschijnlijke de volgende situatie spontaan naar boven:
‘Er ligt nog een derde van de cake op tafel. Ik neem hier een vijfde van mee naar school. Welk deel van de cake blijft over?’
Deze situatie geeft echter aanleiding tot de bewerking \frac{1}{3}-\frac{1}{5}\cdot \frac{1}{3} en deze wiskundige vertaling past dus niet bij de bewerking \frac{1}{3}-\frac{1}{5}. Wel passend is bijvoorbeeld:
‘Er ligt een derde van een cake op tafel. Ik neem altijd een vijfde van een hele cake mee naar school. Welk stuk van de cake blijft over?’
Je kunt leerlingen hiervan op twee manieren bewust maken. Ofwel kies je er voor om zelf een situatie te geven en die kort te bespreken. Ofwel geef je de bewerking en laat je de leerlingen zelf een situatie zoeken die past bij die bewerking met breuken.
Bij de eerste aanpak speel je op veilig en zorg je ervoor dat je zelf de situatie goed in de hand houdt. Je ruimt een mogelijk probleem op voorhand al uit de weg.
Bij de tweede manier komt er gegarandeerd een leerling met een verkeerd voorstel. Het zal fout lopen en je haalt je sowieso problemen op de hals.
Om de tweede situatie toe te laten, heb je een hogere ongemaksdulding nodig. De kans is immers veel groter dat er momenten van chaos ontstaan. Op dat moment maak je impliciet zichtbaar hoe jij met onopgeloste problemen omgaat en straal je uit dat het acceptabel is om een onopgelost probleem te hebben. Dat impliciet voorleven helpt leerlingen om dit bij zichzelf ook toe te laten.
5.2 Doorzettend vermogen
Test jezelf
Vul, voor je verder leest, de onderstaande verhouding in:
Intelligentie = ……………………..% inspanning + ……………………..% aanleg.
In onze zoektocht om ongemaksdulding te verhogen kwamen we uit bij psychologe Carol Dweck (Kumps. s.d.). Zij onderzoekt waarom sommige mensen doorzettend vermogen vertonen in moeilijke situaties terwijl anderen daar vooral hulpeloosheid vertonen. Volgens haar is niet ‘het krijgen van lof’ of ‘het ervaren van succes’ maar wel de manier waarop je naar intelligentie kijkt de motor om door te zetten in moeilijke situaties. Ze gaat uit van twee verschillende theorieën over intelligentie. We lichten ze beide kort toe.
Fixed mindset
Sommige mensen geloven dat intelligentie of slimheid een onveranderlijke, aangeboren eigenschap is. Ze hebben er een bepaalde hoeveelheid van en dat is het dan. Je bent slim of je bent het niet. Dweck noemt dit een fixed mindset of de theorie van de vaste intelligentie.
Dit heeft veel gevolgen voor leerlingen. Leerlingen kunnen zich afvragen hoeveel ze bezitten van deze vaste intelligentie. Het kan ervoor zorgen dat leerlingen het als een prioriteit zien om te laten merken dat ze er voldoende van hebben. Ze moeten slim overkomen en mogen kost wat het kost nooit dom lijken. Ze hebben een imago hoog te houden.
Een taak of een opdracht is een middel waarmee je je ‘slimheid’ zichtbaar kan maken. Inspanningen, iets niet kunnen, moeilijkheden, tegenslag kunnen ertoe leiden dat ze hun intelligentie in twijfel trekken. Een uitdaging, een probleem voelt aan als een bedreiging voor de zelfwaarde. Deze leerlingen zoeken opdrachten die gemakkelijk zijn en weinig inspanning vragen en vermijden moeilijke opdrachten. Wanneer ze moeilijkheden tegenkomen, geven ze snel op.
Growth mindset
Voor anderen is intelligentie geen vaste eigenschap, niet iets dat je hebt, maar wel iets dat je kunt ontwikkelen door bij te leren. Dweck noemt dit de growth mindset of de theorie van de vervormbare intelligentie omdat intelligentie hierin afgeschilderd wordt als iets dat door middel van inspanning kan groeien.
Dit betekent niet dat mensen die de groeitheorie hanteren, ontkennen dat er verschillen zijn tussen mensen wat betreft hun kennis of wat betreft de snelheid waarmee zij zich bepaalde zaken eigen maken. Het betekent enkel dat deze mensen ervan uitgaan dat iedereen, met inspanning en begeleiding, in staat is om zijn/haar intellectuele capaciteiten te vergroten.
Ook dit denkbeeld heeft grote gevolgen voor leerlingen. Het zorgt ervoor dat ze willen bijleren. Als je gelooft dat je je eigen intelligentie kunt verhogen, waarom zou je dat dan niet doen? Waarom tijd verliezen met je zorgen te maken over hoe dom of hoe slim je overkomt, terwijl je gewoon slimmer kunt worden? Als ze deze visie hanteren, dan zullen zelfs leerlingen met weinig vertrouwen in hun intelligentie hard werken bij uitdagingen, ze zullen zich met overgave wijden aan een moeilijke taak en ze zullen dat volhouden.
Een taak of een opdracht is een middel waarbij ze inspanningen leveren om iets nieuws onder de knie te krijgen. Het zelfwaardegevoel is totaal verschillend in de groeitheorie. Bij deze mindset stijgt je zelfwaardegevoel wanneer je, in iets dat je waardevol acht, volledig opgaat en wanneer je daartoe al je mogelijkheden tot het uiterste benut.
Zelfwaardegevoel is dan niet iets dat we aan anderen kunnen geven door hen te vertellen hoe intelligent ze zijn. Het is iets waartoe we anderen uitrusten, zodat ze het zelf kunnen verwerven: door hen aan te leren dat bijleren belangrijker is dan slim overkomen, door hen te leren om van uitdagingen en inspanningen te genieten en om fouten te beschouwen als de weg naar beheersing van nieuwe kennis.
Om even terug te komen op het bovenstaande testje: voor de personen met een growth mindset was de verhouding was eerder 65% inspanning en 35% aanleg. Voor proefpersonen met een fixed mindset was het net andersom.
Rol van de leraar
Het meest boeiende aan het onderzoek van Dweck is dat het handelen van de leraar en zijn communicatie effect hebben op hoe leerlingen doorzetten. We bespreken dit kort.
- De manier waarop je over taken of opdrachten spreekt: gaat de taak je bekwaamheid meten (fixed mindset) of zal de taak ervoor zorgen dat je waardevolle dingen bijleert?
- De kracht van het gebruik van het woordje ‘nog’: wanneer een leerling een fout maakt of een slecht cijfer behaalt en je dit benoemt met ‘je kunt het ‘nog’ niet’. Dat wijst erop dat inspanning zal helpen om het te leren. Dit wordt nog versterkt als je aangeeft wat voor acties de leerling kan ondernemen om het te leren.
- De manier waarop je feedback geeft aan leerlingen. Wanneer je zegt ‘Je bent slim, goed, sterk’ geef je persoonsgerichte feedback die de volledige persoon erin betrekt. Dan geef je een signaal dat stuurt naar een fixed mindset. Dit is persoonsgerichte feedback. Wanneer je echter inspanning, verschillende strategieën, vooruitgang en doorzettingsvermogen prijst, stuur je in de richting van een growth mindset. We noemen dit taakgerichte feedback.
5.3 Fouten als bron
Wanneer we de ideeën van Carol Dweck volgen dan is het maken van fouten geen teken van falen maar wel een teken dat je iets probeert te leren. Fouten leveren dikwijls waardevolle informatie op. Ze maken zichtbaar wat er ontbreekt opdat het antwoord een juiste oplossing is. In dat opzicht is het minstens even boeiend om verkeerde oplossingen te bespreken als om correcte oplossingen te tonen. Wanneer je als leraar deze status geeft aan fouten, wordt het een stuk veiliger om een verkeerd antwoord te geven.
Zelf geef ik fouten altijd een ruime plaats in mijn lessen. Geregeld breng ik verschillende oplossingen aan bord en bespreek de elementen die goed waren en waarom sommige dingen niet kloppen. Zelfs hoe het komt dat leerlingen die fouten maken. Het helpt om te herkennen welke elementen je soms op het verkeerde been zetten. Na vele jaren ervaring weet ik welke opgaven vaak fout lopen. Ik kies er net voor om die opgaven te maken en daardoor de fouten uit te lokken. Gewoonlijk vermeld ik erbij: ‘Ik ben blij je deze fout maakte. Daardoor hebben we dit besproken wat ervoor kan zorgen dat je in de toekomst deze fout niet meer maakt.’ Want het is natuurlijk de bedoeling dat leerlingen leren uit fouten.
Bij de oplossing van het angula-probleem maakten we al zichtbaar hoe een leraar een voorbeeldfunctie kan opnemen voor het omgaan met zijn eigen fouten. Hieronder vind je een tweede voorbeeld dat illustreert hoe rijk fouten kunnen zijn.
Helling 4
Opgave
Bepaal de x-coördinaten van de punten van de grafiek van de functie met voorschrift f(x)=\frac{3}{4}x^4+\frac{1}{3}x^3-6x^2 waar de helling gelijk is aan 4.
Een leerling noteert de onderstaande oplossing.
Gegeven
f(x)=\frac{3}{4}x^4+\frac{1}{3}x^3-6x^2
Helling in de punten is 4.
Gevraagd
x-coördinaten van deze punten?
Oplossing
- Een schets helpt om het probleem beter te begrijpen
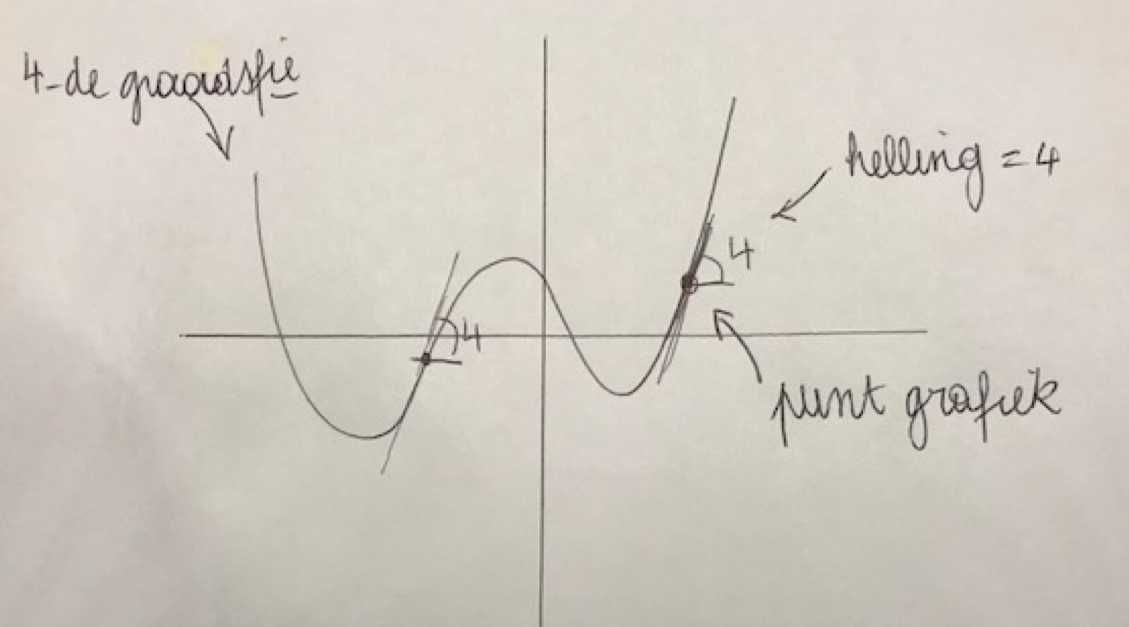
- Een plan opstellen
‘Een helling gelijk aan vier’ vertalen we naar het zoeken waar de afgeleide gelijk is aan vier. Of f'(x)=4. Dat betekent dus eerst de afgeleide functie berekenen en dan de oplossingen van de bovenstaande vergelijking zoeken.
- Het plan uitvoeren
f'(x)=3x^3+x^2-12x
f'(x)=3x^3+x^2-12x levert als oplossingen x=2 of x=-2.
De grafiek heeft een raaklijn met richtingscoëfficiënt gelijk aan 4 in en in .
Controleren van de oplossing
De oplossing lijkt te kloppen met de schets. Daar staan twee evenwijdige raaklijnen getekend.
Foutenbespreking
Ik kies er voor om dit klassikaal te bespreken. Ik stel voor om de grafiek en de raaklijnen in 2 en -2 in GeoGebra te tekenen. Dat levert het onderstaande resultaat. De leerlingen merken al snel op dat je tussen -1 en 0 een derde raaklijn kunt tekenen die ook evenwijdig is met de andere twee. Er is dus iets fout gelopen.
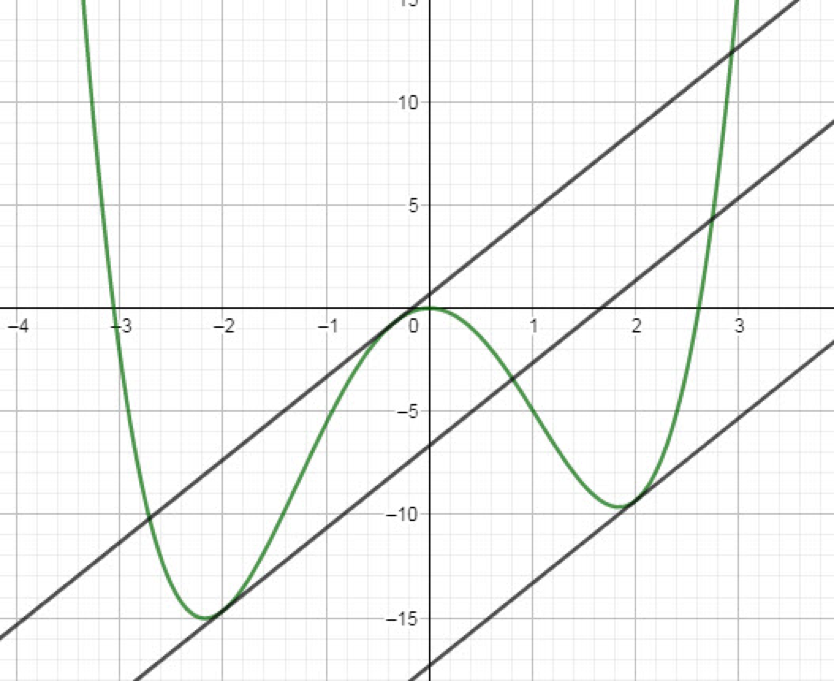
Wat liep er fout en hoe kwam het dat dat fout liep?
Wanneer ik vraag hoe ze de oplossingen van de vergelijking f'(x)=4 gevonden hebben, blijkt dat ze de delers van 4 invulden in de vergelijking. 2 en -2 waren getallen die een oplossing gaven. De andere delers leverden geen oplossing op. Wanneer ik het functieverloop van f'(x)-4=3x^3+x^2-12x-4 laat tekenen worden de drie nulpunten snel zichtbaar. Dit is een goed moment om het aantal nulpunten van een derdegraadsfunctie opnieuw te bespreken: ofwel één ofwel drie, waarbij twee van de drie eventueel kunnen samenvallen.
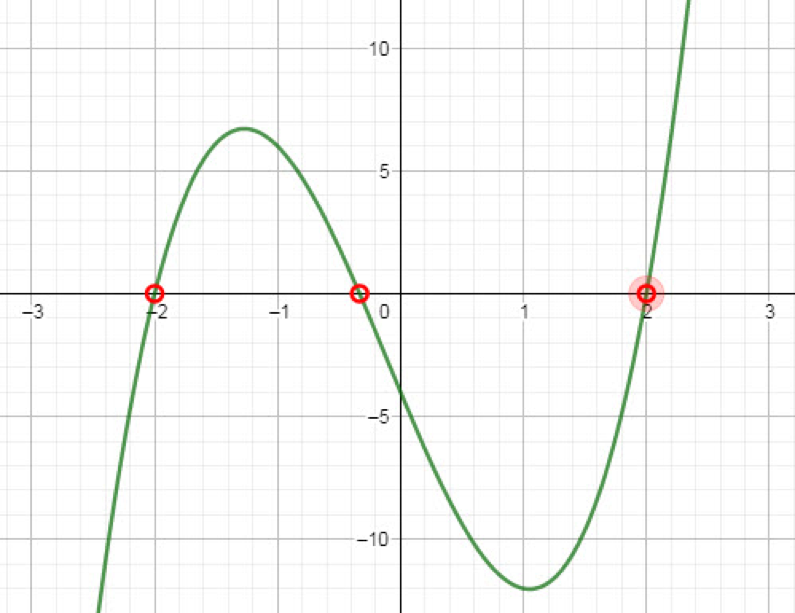
Een tweede interessante vraag is hoe het komt dat de schets ons op het verkeerde been zette? Dat is even zoeken voor de leerlingen. In de schets is een raaklijn getekend die door een buigpunt van de functie gaat. Dat betekent dat deze raaklijn op de schets een speciaal geval is: f'(x)-4 zou er twee samenvallende oplossingen hebben. Een mooi leermoment over hoe redeneren op schetsen soms toch gevaren inhoudt.
Langs mijn neus weg, merk ik nog even op dat op de schets het getalletje 4 bij de helling ook wat raar overkomt. Je kunt daar beter rico=4 noteren en in plaats van de hoeken de onderstaande aanduiding gebruiken. Zo hebben we ineens de betekenis van een richtingscoëfficiënt herhaald.
![]()



 Onder de loep
Onder de loep
