Verhelderende bewijzen

Elke wiskundige heeft het wel eens meegemaakt: je hebt een bewijs gelezen en begrepen maar je begrijpt nog steeds niet waaróm de stelling geldt. Alle stappen van een bewijs doorgronden is jammer genoeg niet voldoende om de stelling zelf te doorgronden. Dat laatste vergt inzicht in de achterliggende samenhang van eigenschappen. Gelukkig zijn er ook bewijzen die wel blootleggen waarom een stelling klopt. Zulke bewijzen bieden ook voor leerlingen een meerwaarde.

Hieronder geef ik er twee uit analytische meetkunde, één voor het kenmerk van loodrechte stand en één voor de formule voor de afstand van een punt tot een rechte. Het tweede bewijs is verwant aan het bewijs dat in Deprez & Verscheure (2008) gegeven werd maar deze versie is korter en sluit misschien nog beter aan bij het referentiekader van leerlingen van het \(4^{de}\) jaar van het secundair onderwijs.

Beide bewijzen vergen een constructie als voorbereiding, maar de berekeningen zelf zijn zeer beperkt zodat de formule bijna rechtstreeks uit de constructie volgt.

Loodrechte stand van rechten

Het bewijs van de stelling wordt gegeven voor twee rechten door de oorsprong die niet evenwijdig zijn met de assen.

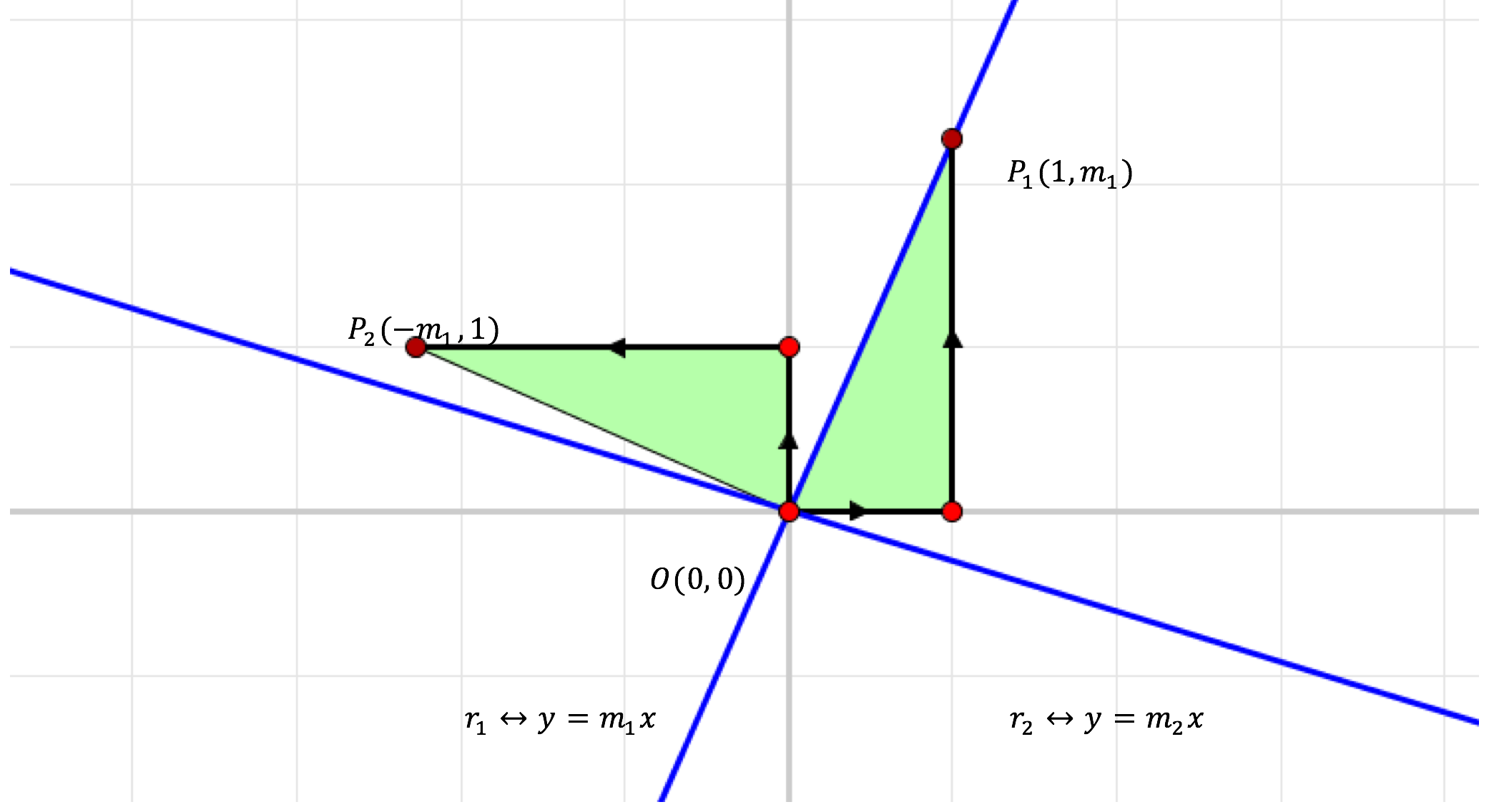
Figuur 1 Loodrechte stand van rechten

In figuur 1 is de richtingscoëfficiënt \(m_1\) van de rechte \(r_1\) positief. Voor een negatieve richtingen \(m_1\) is de figuur lichtjes anders maar gaat de redenering ook perfect op.

Uit de constructie van de punten \(P_1\) en \(P_2\) volgt onmiddellijk dat de gekleurde driehoeken congruent zijn en dat de dragers van hun zijden twee aan twee loodrecht staan op elkaar. De kern van het bewijs van de stelling over de loodrechte stand komt dan neer op de onderstaande redenering.

\( r_1 \perp r_2 \Leftrightarrow P_2 \in r_2 \Leftrightarrow 1=m_2 \cdot (-m_1) \)

Men kan de redenering ook betrekken op de richtingscoëfficiënten.

\(\begin{aligned}
r_1 \perp r_2 \quad &\Leftrightarrow \quad \textrm{rico}(r_2)=\textrm{rico} (OP_2) \\
&\Leftrightarrow \quad m_2=- \frac{1}{m_1}
\end{aligned}\)

In beide gevallen is de laatste formule gelijkwaardig met de gekende formule

\(m_1 \cdot m_2=-1.\)

Afstand van een punt tot een rechte

In de klassieke formule voor de afstand van een punt \(P\) tot een rechte \(u\) wordt de algemene vergelijking van een rechte \(ax+by+c=0\) gebruikt. Gezien het minder voor de hand ligt betekenis te geven aan de coëfficiënten \(a\), \(b\) en \(c\), lijkt het aangewezen de vorm \(y=mx+q\) te gebruiken, waarin de coëfficiënten \(m\) en \(q\) op de grafiek af te lezen zijn. De formule die we moeten bewijzen luidt dan

\(|Pu|=\frac{|mx_P-y_P+q|}{\sqrt{m^2+1}}.\)

Voor het bewijs gebruiken we de constructie van figuur 2, die niet mogelijk is voor de bijzondere gevallen van een rechte evenwijdig met één van de assen maar wel voor alle andere configuraties.

De figuur varieert met de helling van \(u\) en de ligging van \(P\) ten opzichte van \(u\), maar de constructie en alles wat eruit volgt is onafhankelijk van de specifieke configuratie.

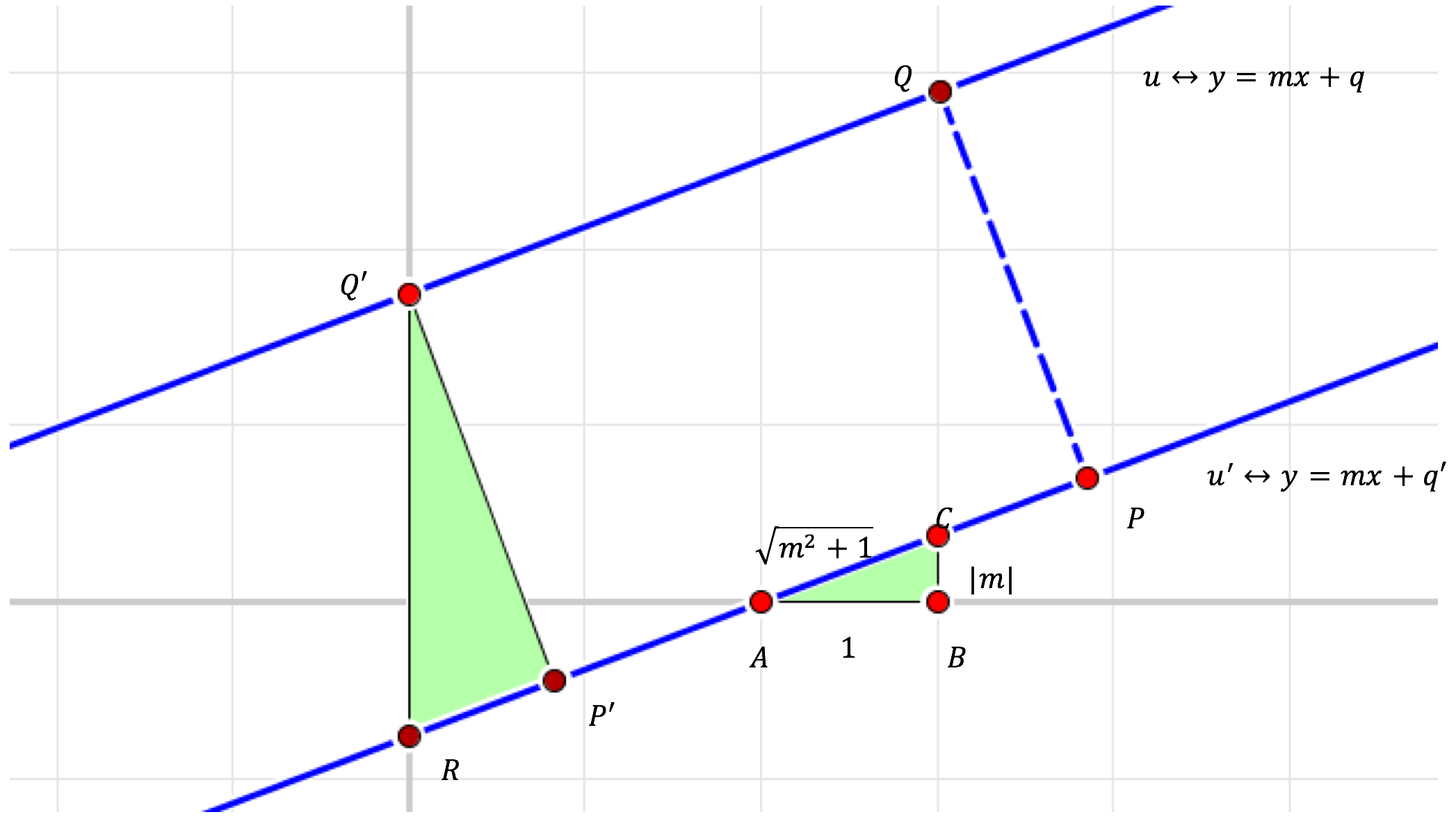
Figuur 2 Afstand van een punt tot een rechte

We overlopen de constructie-elementen:

• \(Q\) is het voetpunt van de loodlijn uit \(P\) op \(u\),
• \(Q’\) is het snijpunt van \(u\) met de \(y\)-as,
• \(u’\) is de rechte door \(P\) evenwijdig met \(u\),
• \(P’\) is het voetpunt van de loodlijn uit \(Q’\) op \(u’\),
• \(R\) is het snijpunt van \(u’\) met de \(y\)-as,
• \(A\) is het snijpunt van \(u’\) met de \(x\)-as,
• \(B\) is het punt op afstand 1 rechts van \(A\),
• \(C\) is het punt op \(u’\) met hetzelfde eerste coördinaatgetal als \(B\).

Als de vergelijking van de rechte \(u\) gegeven wordt door

\(u \leftrightarrow y=mx+q\)

zal de vergelijking van de rechte \(u’\) gegeven worden door

\(u’ \leftrightarrow y=mx+q’.\)

Berekenen we \(q’\) door de coordinaatgetallen van het punt \(P\) in te vullen, dan krijgen we \(q’=-mx_P+y_P.\)

Uit de bovenstaande constructie volgt nu dat \(\Delta P’Q’R \sim \Delta BAC\). Hieruit kunnen we \(|PQ|\) berekenen:

\(\begin{aligned}
|PQ| &= |P’Q’|=\frac{|P’Q’|}{|AB|}=\frac{|Q’R|}{|AC|}\\
&=\frac{|q-q’|}{\sqrt{m^2+1}}=\frac{|q-(-mx_P+y_P)|}{\sqrt{m^2+1}}\\
&=\frac{|mx_P-y_P+q|}{\sqrt{m^2+1}}.
\end{aligned}\)

Op deze manier zien we vrij direct hoe zowel de teller als de noemer in de formule tot stand komen.

Algemene formulering

Merk op dat deze formule gemakkelijk om te vormen is tot de gekende formule door de traditionele omvorming van de vergelijking van de rechte:

\(ax+by+c=0 \quad \Leftrightarrow \quad y=-\frac{a}{b} x-\frac{c}{b}.\)

We voeren de substituties \(m=-\frac{a}{b}\) en \(q=-\frac{c}{b}\) uit in de eindformule uit de vorige paragraaf. Hierdoor verkrijgen we

\(\begin{aligned}
|PQ| &= \frac{|(-\frac{a}{b}) x_P-y_P-\frac{c}{b}|}{\sqrt{(-\frac{a}{b})^2+1}}\\
&= \frac{|a\cdot x_P+b \cdot y_P+c|}{\sqrt{a^2+b^2}}.
\end{aligned}\)

Bijzondere gevallen

De bijzondere gevallen van een rechte evenwijdig met één van de assen kunnen apart behandeld worden. In beide gevallen vinden we de gekende formule terug.

Als \(a=0\) dan loopt de rechte \(u\) evenwijdig met de \(x\)-as.

\(by+c=0 \quad \Leftrightarrow \quad y=- \frac{c}{b}\)

De afstand van \(P\) tot \(u\) wordt op de volgende manier berekend:

\(\begin{aligned}
|PQ| &= \Bigl| y_P- \left( -\frac{c}{b}\right) \Bigr|= \Bigl| y_P+\frac{c}{b}\ \Bigr|\\
&= \frac{| y_P+\frac{c}{b}|\cdot |b|}{|b|}=\frac{|b\cdot y_P+c|}{\sqrt{b^2}}\\
&= \frac{|a\cdot x_P+b \cdot y_P+c|}{\sqrt{a^2+b^2}}.
\end{aligned}\)

Als \(b=0\) dan loopt de rechte \(u\) evenwijdig met de \(y\)-as.

\(ax+c=0 \quad \Leftrightarrow \quad x=- \frac{c}{a}\)

De afstand van \(P\) tot \(u\) kan dan als volgt berekend worden:

\(\begin{aligned}
|PQ| &= \Bigl| x_P- \left( -\frac{c}{a}\right) \Bigr|= \Bigl| x_P+\frac{c}{a}\ \Bigr|\\
&= \frac{|x_P+\frac{c}{a}|\cdot |a|}{|a|}=\frac{|a\cdot x_P+c|}{\sqrt{a^2}}\\
&= \frac{|a\cdot x_P+b \cdot y_P+c|}{\sqrt{a^2+b^2}}.
\end{aligned}\)

Deze twee bijzondere standen van de rechte \(u\) leveren dezelfde afstandsformule op als de algemene stand.

Nabeschouwing

Beide bewijzen uit de analytische meetkunde van het vierde jaar werpen licht op waarom de formules zijn zoals ze zijn. Bewijzen met een soortgelijke opbouw dragen mijn voorkeur omdat zo sterk mogelijk bijdragen tot het inzicht van leerlingen en van lezers in het algemeen.

Bronnen

Deprez, J., & Verscheure, J. (2008). Afstand van een punt tot een rechte. Uitwiskeling 24/2, 6-9.