Een klassieker onder de wiskundige puzzels is de 15-puzzel, die in 1880 uitgevonden en gepatenteerd werd door Noyes Chapman. De uitvinding werd later onterecht geclaimd door de puzzelbedenker Sam Loyd.
In een 4 \times 4-schuifbord zitten 15 verschuifbare tegeltjes in een geordend patroon. Vaak zijn het de getallen van 1 tot 15 die op de tegeltjes zijn afgebeeld maar soms ook zijn het afbeeldingen die in 15 fragmenten zijn onderverdeeld.
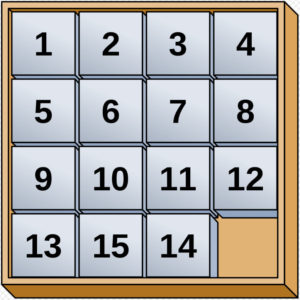
Figuur 1 Een 15-puzzel met getallen
Figuur 2 En 15-puzzel met een afbeelding
Zoals je op deze figuren ziet, ontbreekt er één tegeltje in het schuifbord. Elke tegel die naast de ontbrekende tegel ligt, kan horizontaal of verticaal in de opening geschoven worden. Zo kun je het hele schuifbord door elkaar husselen. Dat doe je bij het begin van de puzzel. De opdracht bestaat er dan in om zo snel mogelijk de beginconfiguratie terug te vinden.
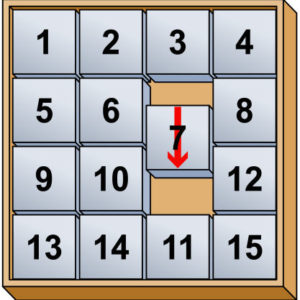
Figuur 3 De 7 wordt omlaag geschoven
Het is aangetoond (zie Brungger e.a., 1999) dat hiervoor ten hoogste 80 tegeltjes moeten worden verschoven. Maar liefst 17 configuraties vereisen deze 80 zetten (zie Korf, e.a., 2005).
Een oplossingsstrategie
Als de tegeltjes van de 15-puzzel op een reglementaire manier door elkaar gehusseld zijn, kan de puzzel altijd opgelost worden door de tegeltjes in omgekeerde zin terug te schuiven. Dit is niet altijd de snelste methode. We beschrijven hier een andere oplossingsstrategie.
Schuif eerst het getal 1 naar de linkerbovenhoek. Het getal 2 kan hier zonder problemen naast geschoven worden. Deze twee tegels blijven nu gedurende de hele oplossing roerloos liggen. Om de 3 en de 4 op hun plaats te krijgen, is er een truc nodig. De hoekjes met hoekstenen vullen is immers niet zo eenvoudig. Schuif eerst de 4 naar de derde plaats van de bovenste rij en zorg ervoor dat de 3 hieronder kan. Manoeuvreer het lege vakje naar de rechterbovenhoek. Schuif tot slot de 4 naar rechts en de 3 omhoog en de eerste rij is OK.
Voor de tweede rij met de 5, 6, 7 en 8 kun je analoog te werk gaan. Maar voor de derde rij is er niet genoeg plaats om deze strategie vol te houden. Daarom ordenen we de tegels nu van links naar rechts. Eerst zetten we de 9 en de 13 op hun plaats. Hiervoor gebruiken we dezelfde truc als hierboven. Schuif de 13 naar de eerste plaats van de derde rij en zorg ervoor dat de 9 hier rechts naast kan. Laat het lege vakje opschuiven tot het linksonder zit. Duw daarna de 13 naar onder en de 9 naar links. Zo zitten deze vakjes op hun plaats. Op dezelfde manier ordenen we de 10 en de 14.
Alleen de rechterbenedenhoek met de getallen 11, 12 en 15 moet nu nog geordend worden. Als je de 11 en het lege vakje naar de correcte positie schuift dan staan de 12 en de 15 automatisch op hun juiste plaats. Dat bewijzen we hieronder. Immers, een configuratie waarbij alleen de 15 en de 12 verwisseld zijn, kan nooit bereikt worden door tegeltjes op een normale manier te verschuiven.
Merk op dat deze strategie ook geldt voor gelijkaardige schuifborden van een groter formaat.
De 15-14-puzzel kan niet opgelost worden: een bewijs door invariantie
Als twee tegeltjes met een koevoet uit het schuifbord gebroken worden en ze er verwisseld weer in worden gemonteerd, dan kan het bord nooit meer in de oorspronkelijke configuratie geschoven worden. Meestal wordt dit geillustreerd door de 15-14-puzzel waarbij de 14 en 15 van plaats gewisseld zijn. We bewijzen hieronder dat het niet mogelijk is om deze puzzel terug te schuiven naar de oorspronkelijke configuratie met oplopende getallen.
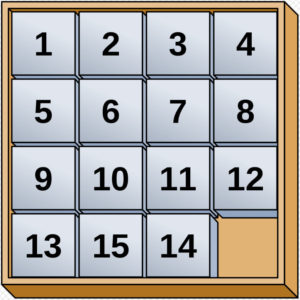
Figuur 4 De 15-14-puzzel
We bewijzen dit door een getal te construeren dat invariant blijft tijdens het schuiven. De invariant ontstaat uit de som van drie getallen:
- het aantal verwisselingen van twee tegeltjes of van een tegeltje en een leeg hokje (1)
- het aantal rijen dat het lege vakje uiteindelijk verwijderd is van rechtsonder (2)
- het aantal kolommen dat het lege vakje uiteindelijk verwijderd is van rechtsonder (3)
Is deze som even dan is de invariant gelijk aan 1, is ze oneven dan is de invariant gelijk aan -1.
Eerst gaan we na dat dit getal werkelijk invariant blijft tijdens het schuiven. Dit is het geval bij een horizontale verschuiving want (1) neemt bij elke horizontale verschuiving met 1 toe en (3) neemt met 1 toe of af. De som van (1), (2) en (3) behoudt dus de pariteit. Als ze even was, blijft ze even. Als ze oneven was, blijft ze oneven. Bij een verticale verschuiving neemt (1) met 1 toe en neemt (2) met 1 toe of neemt (2) met 1 af. Ook hier blijft de pariteit van de som van (1), (2) en (3) behouden.
De beginconfiguratie met 14 en 15 in opklimmende volgorde heeft invariant 1. Er zijn immers geen verwisselingen gebeurd en het lege vakje is 0 rijen en 0 kolommen verwijderd van rechtsonder. Als we alleen de 14 en de 15 verwisselen, wordt de invariant -1. Er is immers 1 verwisseling gebeurd en het lege vakje is 0 rijen en 0 kolommen verwijderd van rechtsonder. Een invariant 1 kan nooit in de invariant -1 overgaan enkel door tegeltjes te verschuiven. Vandaar dat de 14-15-configuratie niet volgens de spelregels kan overgaan in de 15-14-configuratie. Omgekeerd is het uiteraard ook niet mogelijk.
Als we de tegeltjes uit het schuifraam mogen halen, zijn er in totaal 16! manieren om ze terug te zetten. Precies de helft van dit aantal heeft invariant 1, de andere helft heeft invariant -1. Alleen de configuraties met invariant 1 kunnen door te schuiven uit de oorspronkelijke 15-puzzel verkregen worden. Dat zijn er in totaal 10\; 461 \;394\; 944\; 000.
Bronnen
- Korf, R., Schultze, P. (2005). Large-scale parallel breadth-first search. Proceedings of the 20th National Conference on Artificial Intelligence (AAAI-05), 1380-1385.
- Brungger, A., Marzetta, A., Fukuda, K., Nievergelt, J. (1999). The parallel search bench ZRAM and its applications. Annals of Operations Research 90. 45-63.
- Wm. Woolsey Johnson, & Story, W. (1879). Notes on the “15” Puzzle. American Journal of Mathematics, 2(4). 397-404. doi:10.2307/2369492, ISSN 0002-9327, JSTOR 2369492.
Foto met dank aan Mr Puzzle – https://www.youtube.com/watch?v=DgkeoRf9o-4





 Onder de loep
Onder de loep