Luka Hartman, Mathias Tilkin en Parfaite Zikpi zijn laatstejaarsstudenten educatieve bachelor secundair onderwijs aan de hogeschool UCLL (Diepenbeek). Dit artikel is een ingekorte versie van een workshop voor medestudenten en collega’s die zij ontwierpen in het kader van hun afstudeerproject onder begeleiding van Michel Roelens.

In de workshop, die zowel online als fysiek doorging, gebruikten zij onder meer een interactieve Nearpod-presentatie, waarmee alle deelnemers tegelijk konden antwoorden of oplossingen tekenen.

1. Inleiding

Met deze workshop willen wij jullie een eerste kennismaking bieden met een stuk van de grafentheorie. De grafentheorie is een groeiend vakgebied binnen de (discrete) wiskunde met toepassingen in verscheidene gebieden, waaronder de informatica en de besliskunde. Bovendien zal de grafentheorie vanaf schooljaar 2021-2022 ook een onderdeel zijn van de leerplannen tweede graad (zie o.a. Ontwerpleerplan Wiskunde C tweede graad D-finaliteit, 2021). Naast de grafentheorie in het leerplan, is er ook een onderdeel ‘computationeel denken’. Dit onderdeel sluit mooi aan bij de grafentheorie vanwege de algoritmes.

Een luchtfoto of een kaart van een stad, bv. Hasselt, bevat veel informatie. Voor wie enkel geïnteresseerd is in de verschillende manieren om van een plaats \(A\) naar een plaats \(B\) te gaan, volstaat het patroon van de straten en kruispunten. Wanneer we binnen de kleine ring van Hasselt alle kruispunten voorstellen door punten en de straten door lijnen, dan krijgen we wat we in de wiskunde een graaf noemen (figuur 1).

Een graaf is een schematische weergave van een aantal punten (die bijvoorbeeld kruispunten, huizen, plaatsen, stations… voorstellen), die met elkaar verbonden worden door lijnen (die bijvoorbeeld straten, leidingen, wegen, rails… voorstellen). In de volgende paragraaf willen we dit wiskundig definiëren.

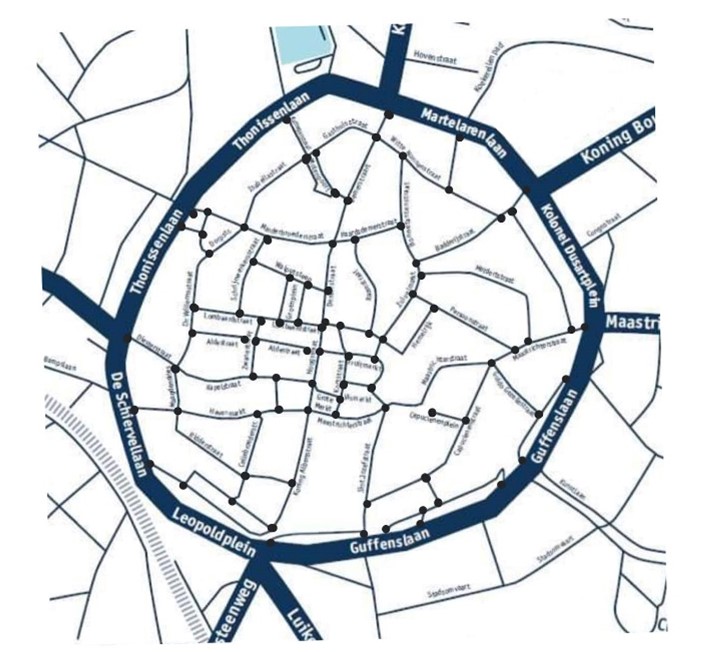
Figuur 1 De binnenstad van Hasselt als een graaf

 

2. Wat is een graaf?

Een graaf \(G\) bestaat uit twee eindige verzamelingen \(V\) en \(E\). De elementen van \(V\) worden knopen genoemd, en die van \(E\) bogen. Elke boog verbindt twee knopen. We noteren met \(uv\) (of \(vu\)) de boog die de knopen \(u\) en \(v\) verbindt. De letters \(V\) en \(E\) komen van de Engelse termen vertex en edge. De notatie van de graaf \(G\) met knopenverzameling \(V\) en bogenverzameling \(E\) is:

\(G = (V,E).\)

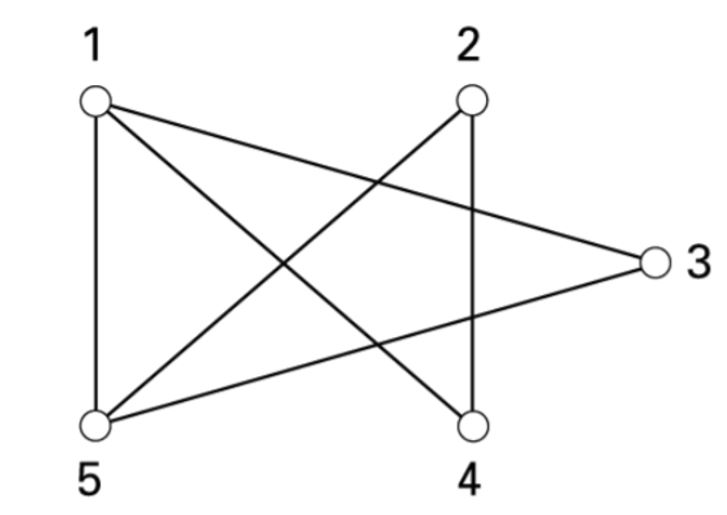
Figuur 2 Een graaf

 

De graaf van figuur 2 heeft als knopenverzameling \(V=\{1, 2, 3, 4, 5\}\). De bogenverzameling is \(E=\{12, 13, 14, 24, 34, 45\}\) (lees: één twee, één drie…). In de volgende werktekst oefenen de deelnemers op deze notatie. Daarnaast wordt verduidelijkt dat dezelfde grafen er toch heel anders uit kunnen zien.

Begin lesactiviteit

Grafen vergelijken en tekenen

  1. Geef van de onderstaande grafen de knopenverzameling en de bogenverzameling. Wat valt je op?

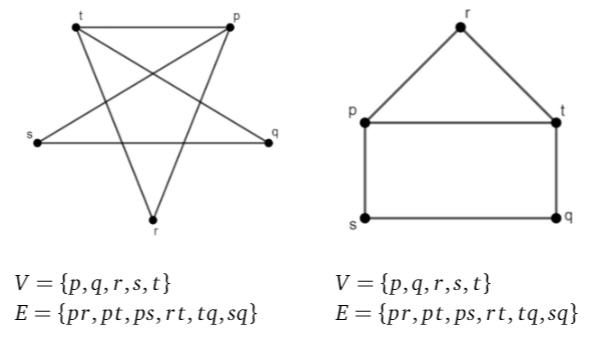
Het zijn dezelfde grafen maar anders voorgesteld.

2. Teken een graaf met \(\{1, 2, 3, 4, 5\}\) als knopenverzameling en waarin twee knopen verbonden zijn als ze ten minste \(2\) verschillen.

Op de plaats van de knopen na, die je vrij mag kiezen, is dit de oplossing:

3. Jan is student aan de hogeschool UCLL te Diepenbeek. Hij komt elke dag met de auto naar de campus en parkeert zijn wagen op de parking van de UHasselt. Helaas komt Jan regelmatig te laat in zijn les. Hij wil daarom op een wiskundige manier zoeken naar de kortste weg. Je ziet hier een plan van de campus in Diepenbeek. Teken een graaf waarbij de knopen de kruispunten voorstellen en de bogen de straten.

 

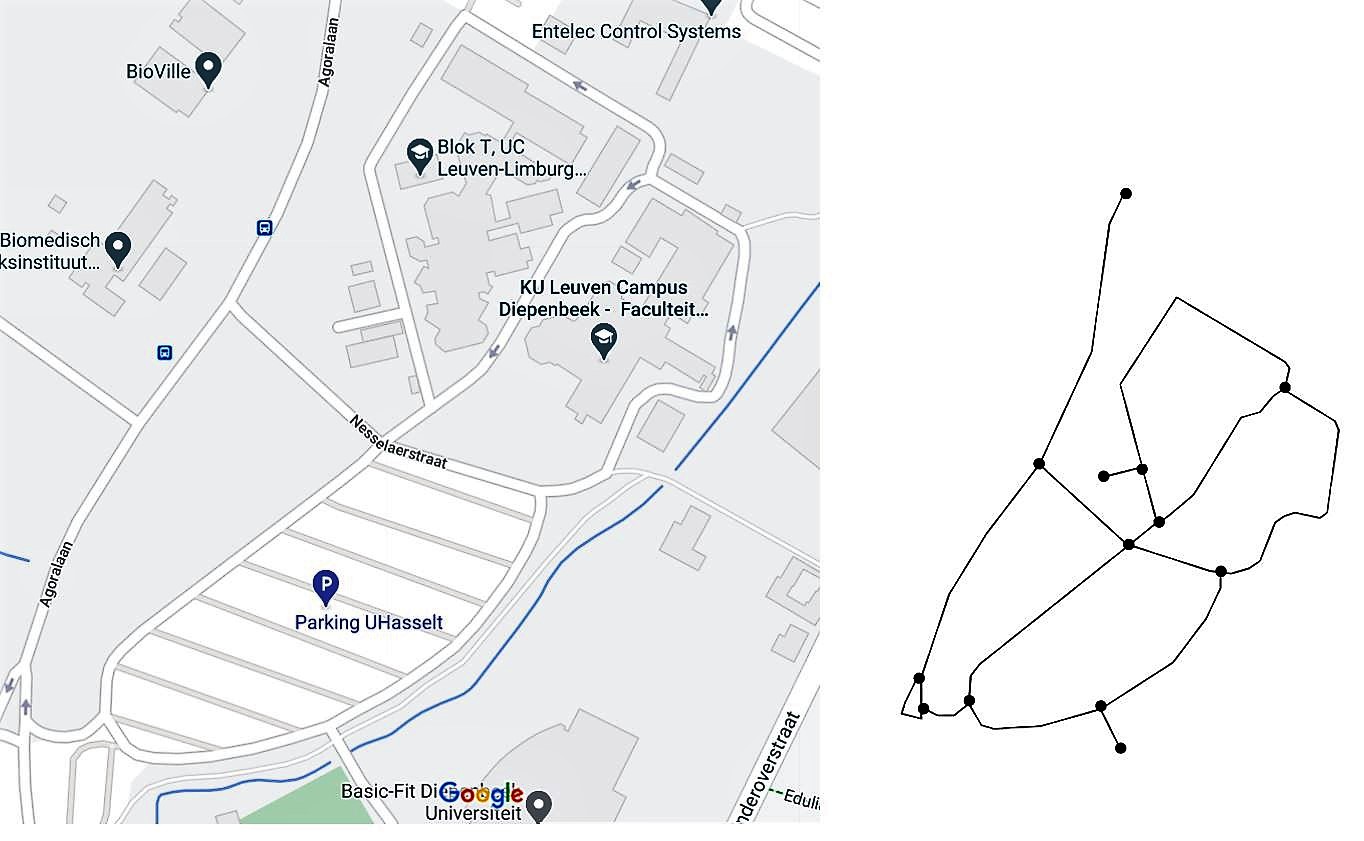
Een mogelijke oplossing staat ernaast. Merk op dat het niet verplicht is om de ”vorm’ van het plan te behouden.

 

3. Soorten grafen

3.1 Gewogen graaf

We willen het kortste pad tussen twee knopen zoeken in een netwerk.

Wat is een pad?

 

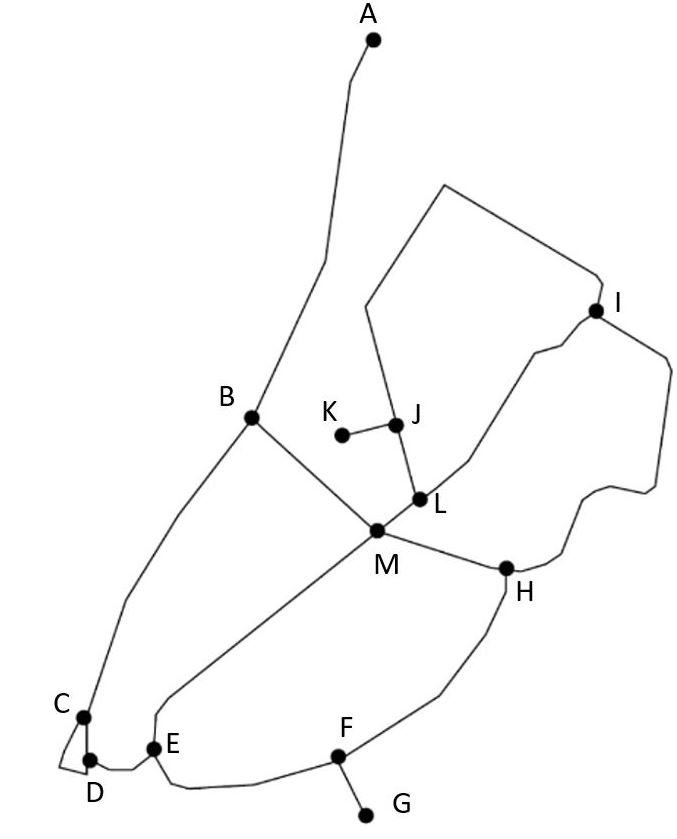
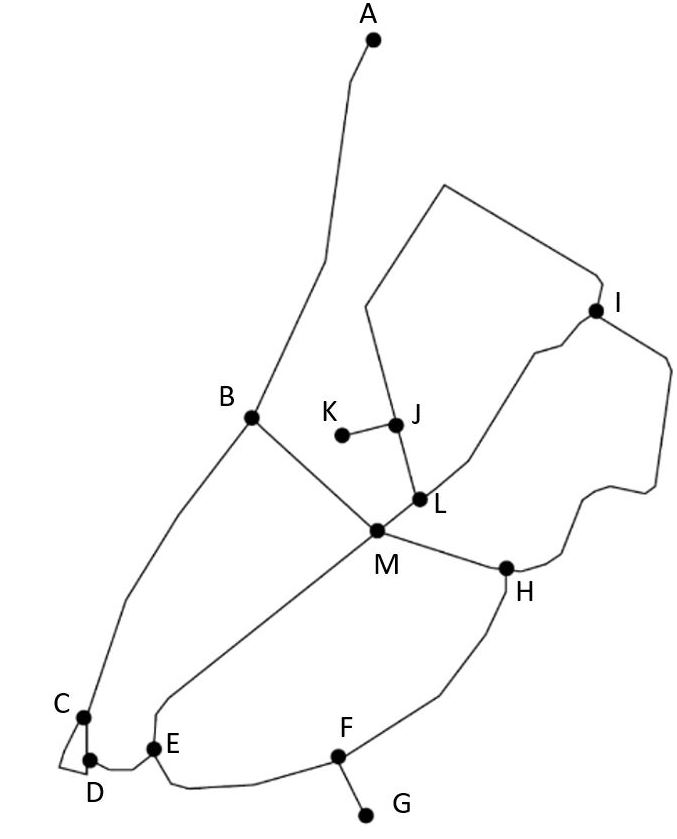
Figuur 3 De graaf van de campus Diepenbeek

 

Een pad tussen twee knopen is een rij knopen beginnend bij de ene knoop en eindigend bij de andere, waarbij tussen elke twee opeenvolgende knopen een boog bestaat. In een pad mag elke knoop hoogstens één keer voorkomen. We noteren een pad door het rijtje opeenvolgende knopen.

In figuur 3 is \(KJIHFG\) een pad van \(K\) naar \(G\). Een ander pad tussen dezelfde knopen is \(KJLMBCDEFG\).

Wat is een netwerk?

Om een kortste pad te zoeken, het pad met de kortste afstand, moet je eerst weten hoe lang de bogen zijn. Het kan ook zijn dat je niet de afstand maar de tijd zo klein mogelijk wilt maken. Dan moet je de reistijd van elke boog kennen.

Een gewogen graaf of netwerk is een graaf waarbij aan elke boog een waarde is toegekend.

In een wegennetwerk zijn de knopen locaties en de bogen wegen. In zo’n netwerk kunnen de waarden van de bogen afstanden voorstellen, of reistijden (afhankelijk van toegelaten snelheden, verkeer, werken…), of kosten (tolwegen…). Deze waarden noemen we de gewichten van de bogen

Begin lesactiviteit

Het kortste pad

Hieronder zie je opnieuw de graaf van de campus Diepenbeek. Links stellen de gewichten de afstand voor (in m), rechts de reistijd (in min).

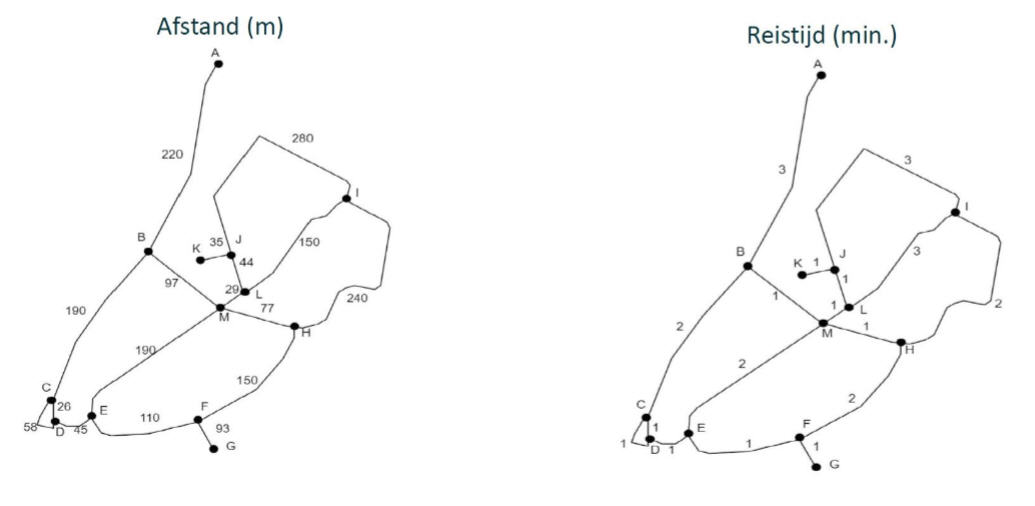
1. Zoek het kortste pad met startpunt \(A\) en eindpunt \(I\) in de graaf met gegeven afstand.

ABMLI

2. Zelfde vraag in de graaf met gegeven reistijd.

ABMHI

3. Wat besluit je hieruit?

De kortste paden kunnen van elkaar verschillen als de gewichten verschillend zijn.

3.2 Samenhangende grafen

Een graaf is samenhangend als tussen elk tweetal knopen een pad bestaat.

Om in een graaf altijd een kortste pad te kunnen vinden tussen een knoop en een andere knoop, moet de graaf uiteraard samenhangend zijn.

 

Begin lesactiviteit

Samenhangende grafen

  1. Hieronder zie je twee grafen. Zijn ze samenhangend of onsamenhangend?

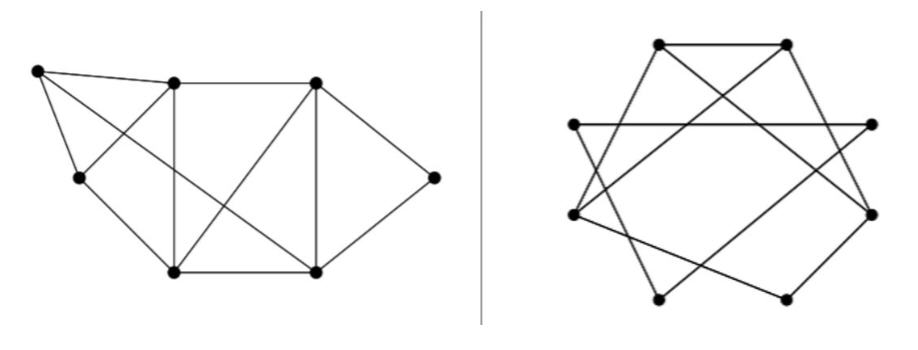
De eerste is samenhangend, de tweede onsamenhangend.

 

4. Dijkstra’s algoritme

Een kortste pad vinden op de campus Diepenbeek is niet zo moeilijk omdat dit een kleine graaf is. Om kortste paden te vinden in heel grote grafen, bijvoorbeeld de kaart van Europa, is een veel systematischer methode nodig die geprogrammeerd wordt in bv. een gps (global positioning system). Het algoritme van Dijkstra is zo’n systematische methode.

Wie was Dijkstra?

Figuur 4 Edsger Wybe Dijkstra

Edsger Wybe Dijkstra (1930-2002) was een Nederlandse wiskundige, theoretische natuurkundige en informaticus. Als programmeur aan het Mathematisch Centrum te Amsterdam ontdekte hij in 1959 zijn kortstepad-algoritme. In 1962 werd hij tot hoogleraar benoemd aan de technische hogeschool Eindhoven. In 1972 ontving hij de Turing Award. Deze prijs wordt soms de Nobelprijs informatica genoemd. Van Dijkstra is de quote:

Informatica gaat net zo min over computers als astronomie over telescopen.

Wat is een algoritme?

Een algoritme is een eindige rij instructies die vanuit een gegeven begintoestand naar een beoogd doel leidt. Je kunt het zien als een recept uit een kookboek. Ook de staartdeling en de oplossing van een tweedegraadsvergelijking met de discriminant zijn algoritmen. Het woord algoritme komt van de naam van de Perzische wiskundige Al-Chwarizmi (9de eeuw).

In feite werkt een computerprogramma op dezelfde manier. Je geeft bijvoorbeeld via je toetsenbord iets in op je computer. Vervolgens voert de computer een algoritme uit en verschijnt het resultaat op je scherm.

Bij het algoritme van Dijkstra vertrekken we van een gewogen graaf en een beginknoop. Dan voeren we een aantal instructies uit en uiteindelijk kennen we het kortste pad van de beginknoop naar elke andere knoop in de graaf.

Hoe werkt het algoritme van Dijkstra?

Bij het algoritme van Dijkstra bezoeken we een voor een alle knopen van de graaf. Ondertussen tellen we de gewichten op vanaf de beginknoop. We maken op elk moment een onderscheid tussen drie soorten knopen: huidige, bezochte en niet-bezochte.

  • De huidige knoop is de knoop die je aan het behandelen bent.
  • De bezochte knopen: deze knopen zijn de huidige knoop geweest en zijn intussen afgehandeld.
  • De niet-bezochte knopen: deze knopen zijn nog niet de huidige knoop geweest.

In het begin speelt de beginknoop de rol van de huidige knoop en zijn alle andere knopen niet-bezocht. Op het einde zijn alle knopen bezocht. Onderweg noteren we bij elke knoop een getal en een letter.

  • Het getal is de kandidaat-afstand, de voorlopige kortste afstand naar deze knoop.
  • De letter geeft aan wat de vorige knoop is in het voorlopige kortste pad.

We omschrijven in het kader hieronder het algoritme op een informele manier. We verduidelijken dit met een eenvoudig voorbeeld waarin we stap voor stap het algoritme toepassen.

Het algoritme van Dijkstra

Stap 1 Neem de beginknoop als huidige knoop. De andere knopen zijn niet-bezochte knopen. We geven de beginknoop waarde \(0\) (de ”afstand van de beginknoop naar zichzelf’) en de niet bezochte knopen waarde \(\infty\).

Stap 2 Bekijk alle niet-bezochte buren van de huidige knoop. Geef aan elk van deze buren als kandidaat-afstand de kleinste waarde van de volgende twee:

  • de waarde die er al bij staat;
  • de waarde van huidige knoop opgeteld met het gewicht van de boog.

(Daarom maken we in het begin gebruik van oneindig: elke andere afstand is dan zeker korter.) Als de nieuwe waarde kleiner is dan wat er al stond, noteer je ook dat je van de huidige knoop komt.

Stap 3 De huidige knoop wordt een bezochte knoop. Kies vervolgens de niet-bezochte knoop met de laagste kandidaat-afstand als huidige knoop. Ga terug verder met stap 2. Indien er geen niet-bezochte buren meer zijn, ga naar stap 4.

Stap 4 Geef het kortste pad van de beginknoop tot elke andere knoop weer. Vermeld telkens ook de gevonden kortste afstand.

We maken dit duidelijk met een voorbeeld: we zoeken het kortste pad van knoop \(A\) naar elke andere knoop in het netwerk van figuur 5.

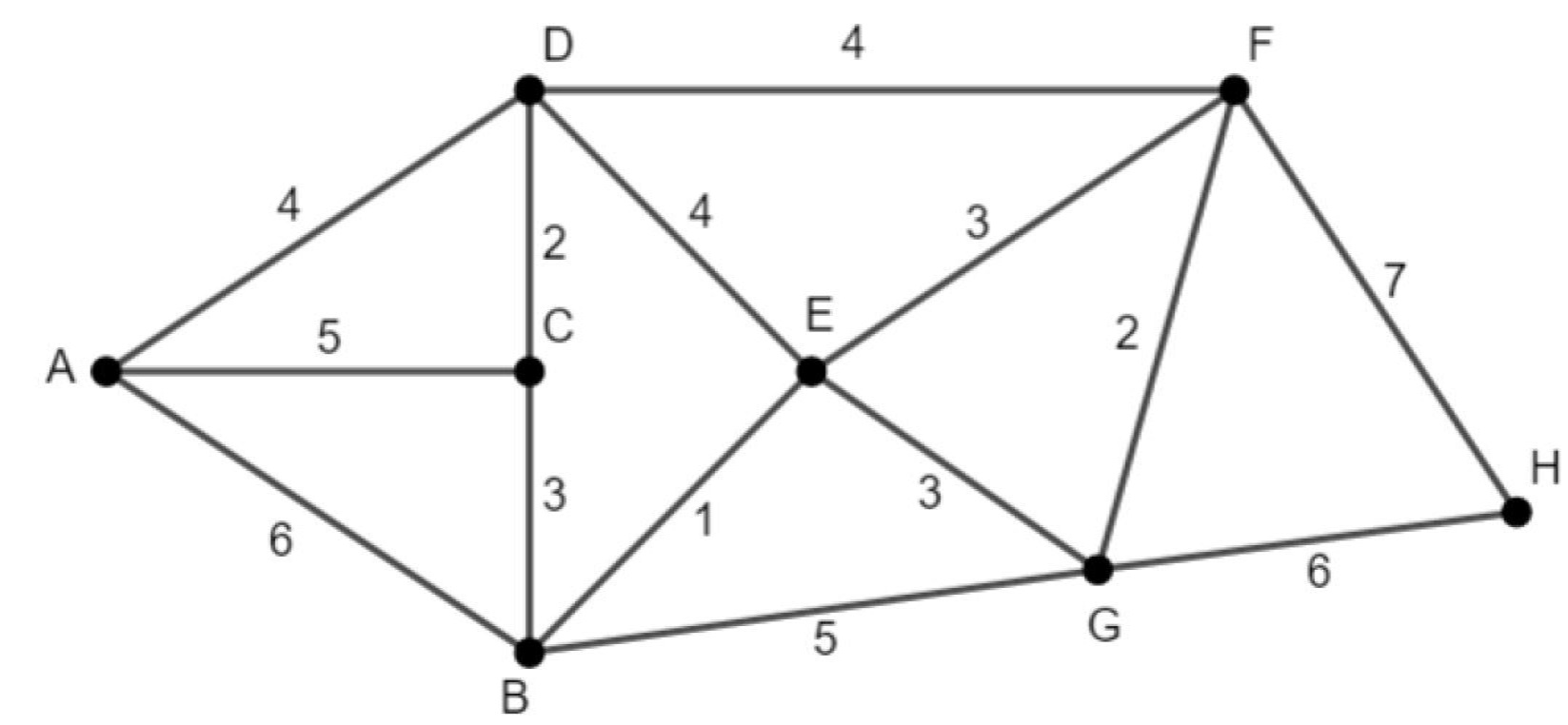
Figuur 5 Het gegeven netwerk

 

Stap 1: De huidige knoop is de beginknoop \(A\): kandidaat-afstand \(0\). Alle andere knopen: kandidaat-afstand \(\infty\) (figuur 6).

 

Figuur 6 Huidige knoop A

 

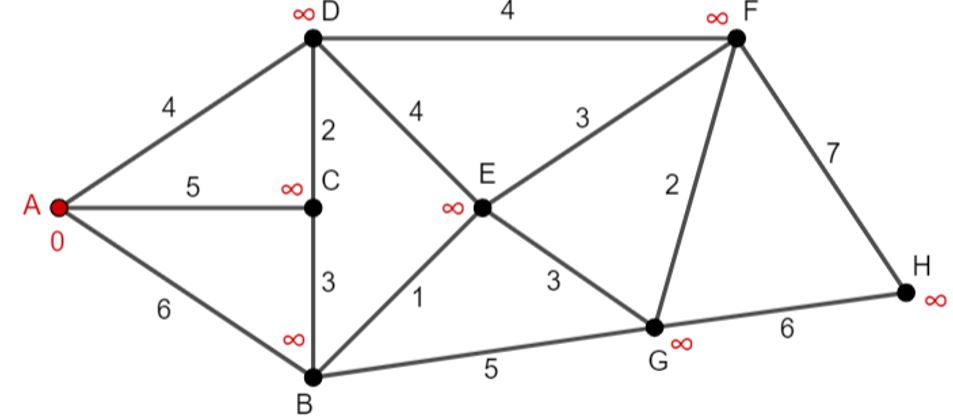
Stap 2: De niet-bezochte buren van \(A\) zijn: \(B: 0+6=6, C:0+5=5\) en \(D: 0+4=4\). Deze waarden zijn kleiner dan wat er stond (namelijk \(\infty\)) en worden er dus bij geschreven als kandidaat-afstanden. We noteren er ook bij dat we van \(A\) komen.

Stap 3: \(A\) wordt bezochte knoop. \(D\) heeft de kortste kandidaat-afstand en wordt de huidige knoop (figuur 7).

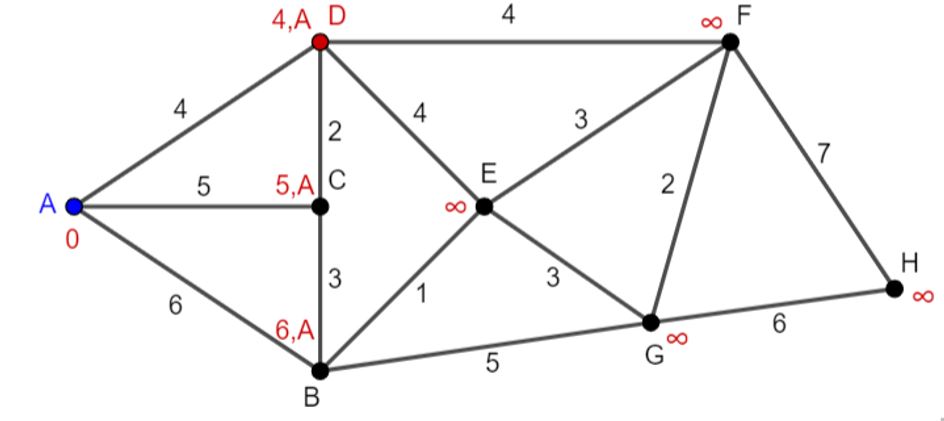
Figuur 7 Huidige knoop D

 

Stap 2: De niet-bezochte buren van \(D\) zijn: \(C: 4+2=6>5\) (waarde blijft \(5\)), \(E: 4+4=8<\infty\), \(F: 4+4=8<\infty\). We noteren bij \(E\) en \(F\) (niet bij \(C\)!) dat we van \(D\) komen.

Stap 3: \(D\) wordt bezochte knoop. \(C\) is de niet-bezochte knoop met de kortste voorlopige afstand en wordt de huidige knoop (figuur 8).

 

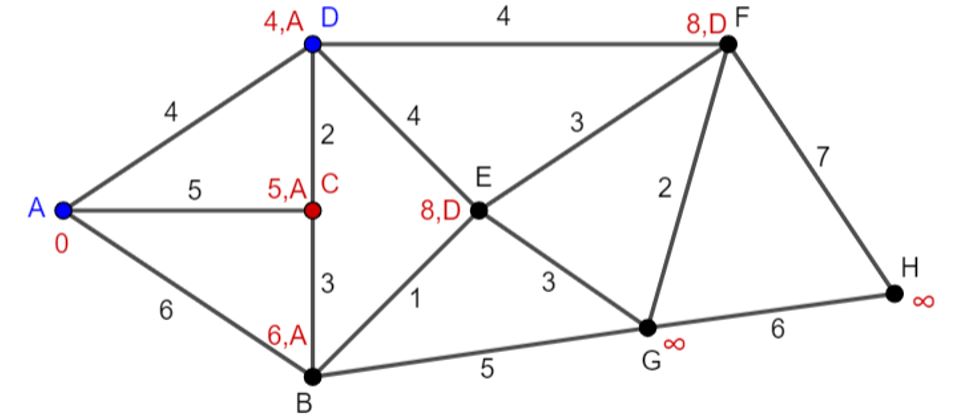
Figuur 8 Huidige knoop C

 

Stap 2: De niet-bezochte buur van \(C\) is \(B: 5+3=8>6\) (waarde blijft \(6\)).

Stap 3: \(C\) wordt bezochte knoop. \(B\) is de niet-bezochte knoop met de kortste voorlopige afstand en wordt de huidige knoop (figuur 9).

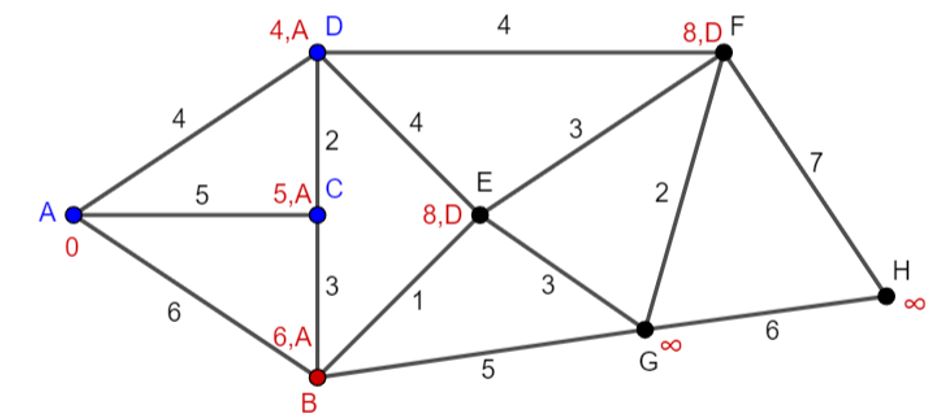
Figuur 9 Huidige knoop B

 

Stap 2: De niet-bezochte buren van \(B\) zijn \(E= 6+1=7<8\) (waarde wordt \(7\) en we noteren dat we van \(B\) komen) en \(G: 6+5=11<\infty\).

Stap 3: \(B\) wordt bezochte knoop. \(E\) wordt de huidige knoop (figuur 10).

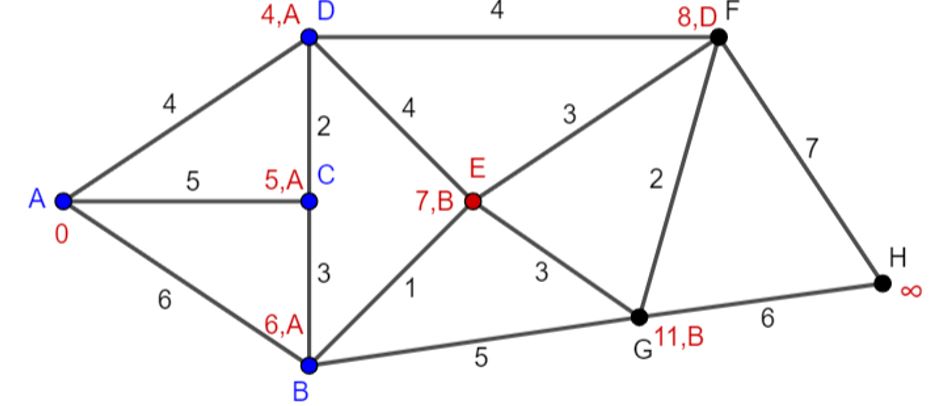
Figuur 10 Huidige knoop E

 

Stap 2: De niet-bezochte buren van \(E\) zijn \(F: 7+3=10>8\) (waarde blijft \(8\)) en \(G: 7+3=10<11\) (waarde wordt \(10\); we komen van \(E\)).

Stap 3: \(E\) wordt bezochte knoop. \(F\) wordt de huidige knoop (figuur 11).

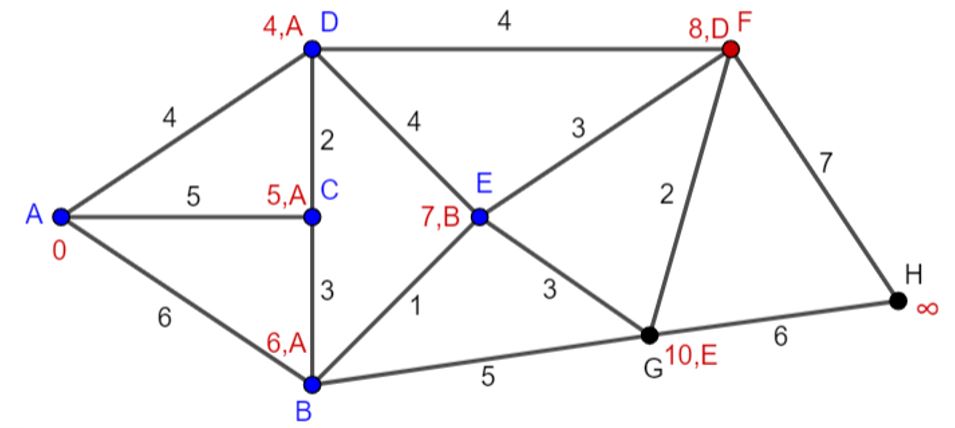
Figuur 11 Huidige knoop F

 

Stap 2: De niet-bezochte buren van \(F\) zijn: \(G: 8+2=10=10\) (waarde blijft \(10\)) en \(H: 8+7=15<\infty\) (waarde wordt \(15\)). Bij \(H\) noteren we dat we van \(F\) komen.

Stap 3: \(F\) wordt bezochte knoop. \(G\) wordt de huidige knoop (figuur 12).

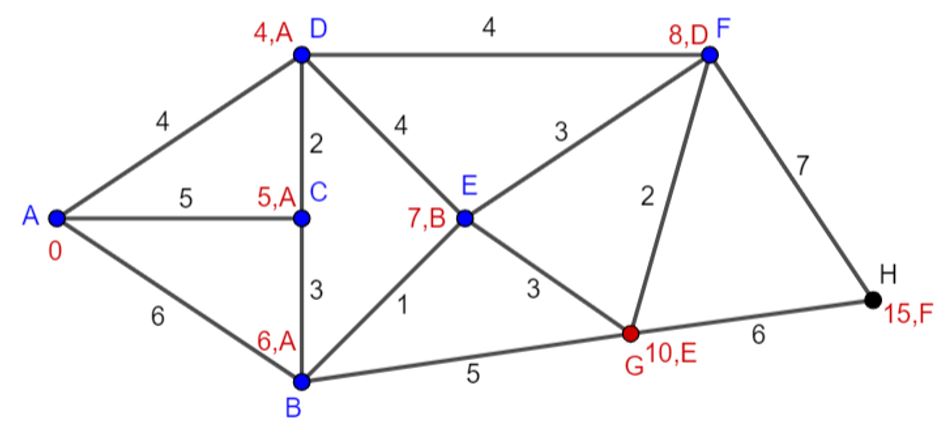
Figuur 12 Huidige knoop G

 

Stap 2: De niet-bezochte buur van \(G\) is \(H: 10+6=16>15\). We passen niets aan.

Stap 3: \(G\) wordt bezochte knoop. \(H\) wordt de huidige knoop (figuur 13). Er zijn geen niet-bezochte buren meer.

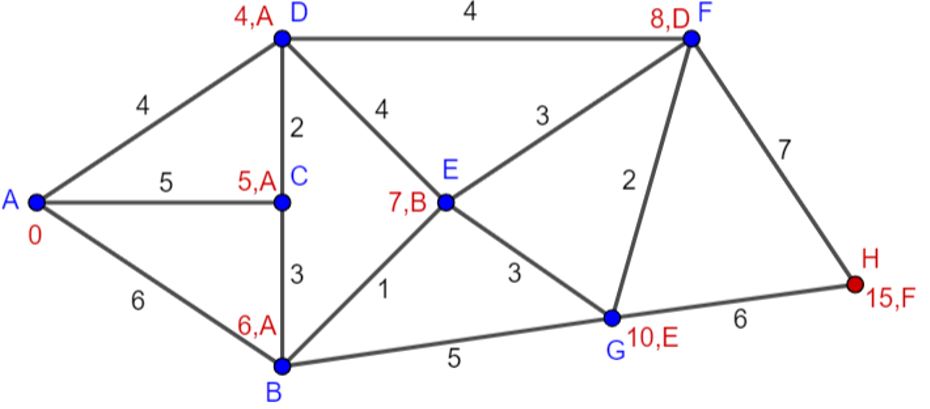
Figuur 13 Huidige knoop H

 

Stap 4: We kunnen de kortste paden vanuit \(A\) naar de andere knopen aflezen. Om bijvoorbeeld de kortste route van \(A\) naar \(H\) af te lezen, kijken we naar de vorig knoop van \(H\), dat is \(F\); de vorige knoop van \(F\) is \(D\) en de vorige knoop van \(D\) is \(A\). Het kortste pad naar \(H\) is dus \(ADFH\) (figuur 14).

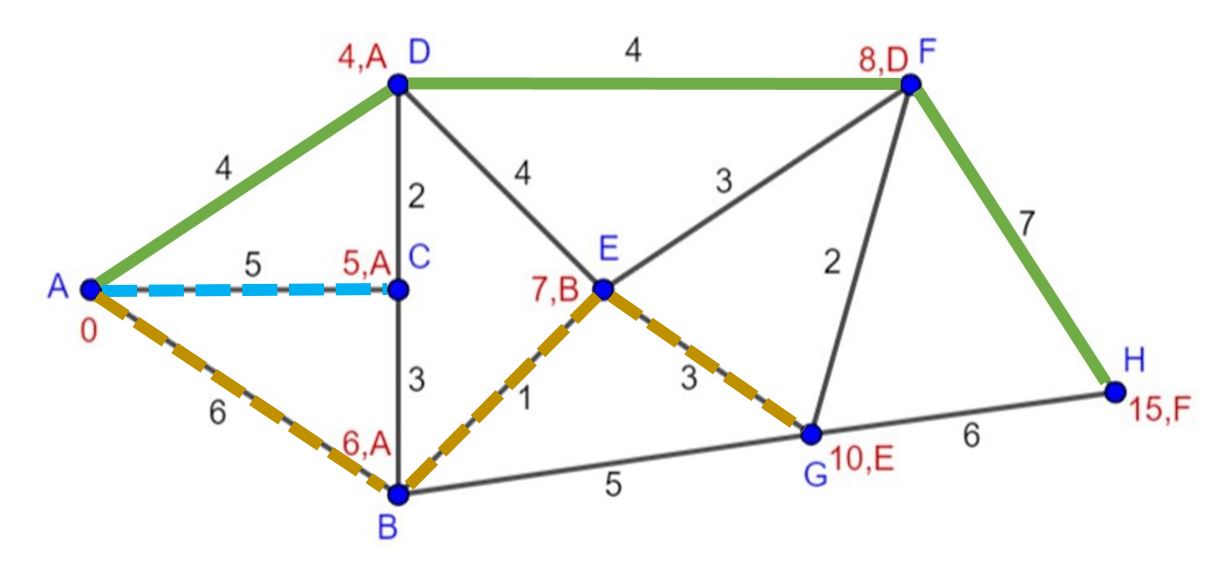
Figuur 14 De kortste paden van A naar de andere knopen

 

Stroomschema

In figuur 15 is het algoritme weergegeven in een stroomschema (of: flowchart). Na het uitgewerkt voorbeeld, is dit stroomschema wel te ontcijferen. Let op: de knopen zijn in dit stroomschema met kleine letters aangeduid.

Zo’n stroomschema kun je bekijken als een tussenstap tussen de informele beschrijving van het algoritme en een computerprogramma dat een computer kan uitvoeren. Analisten ontwerpen stroomschema’s. Programmeurs zetten die om in programmacode.

Het gelijkheidsteken heeft in het stroomschema de betekenis van een toekenning: als er bijvoorbeeld staat \(l(y)=d\), betekent het dat de waarde \(d\) wordt toegekend aan de voorlopige kortste afstand naar knoop \(y\). Let op: in de wiskunde is de gelijkheid symmetrisch (als \(x=y\) dan is ook \(y=x\)); hier niet: de waarde die in het rechterlid staat ken je toe aan het linkerlid, niet omgekeerd.

 

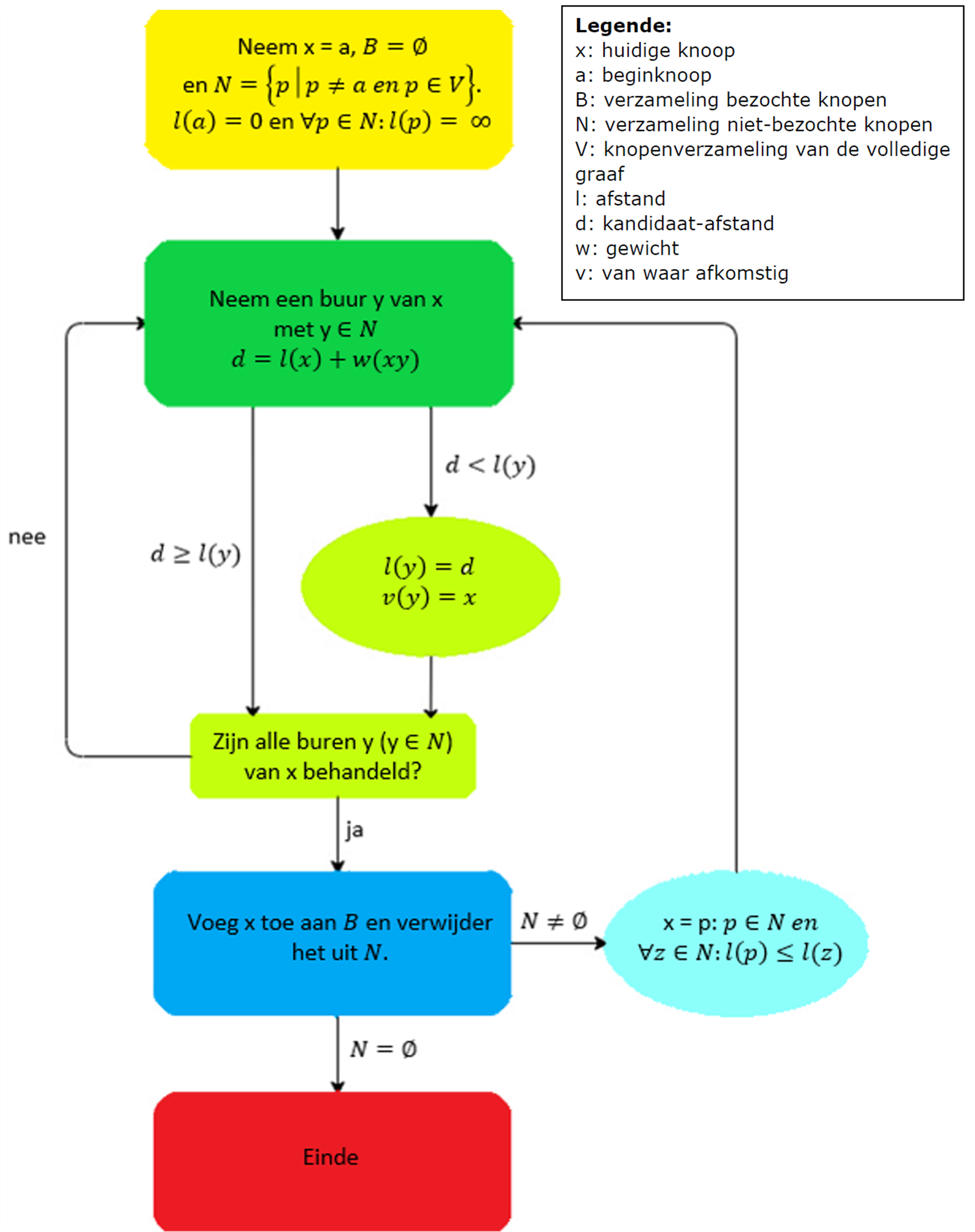
Figuur 15 Stroomschema van het algoritme van Dijkstra

 

Begin lesactiviteit

Het algoritme toepassen op een iets grotere graaf

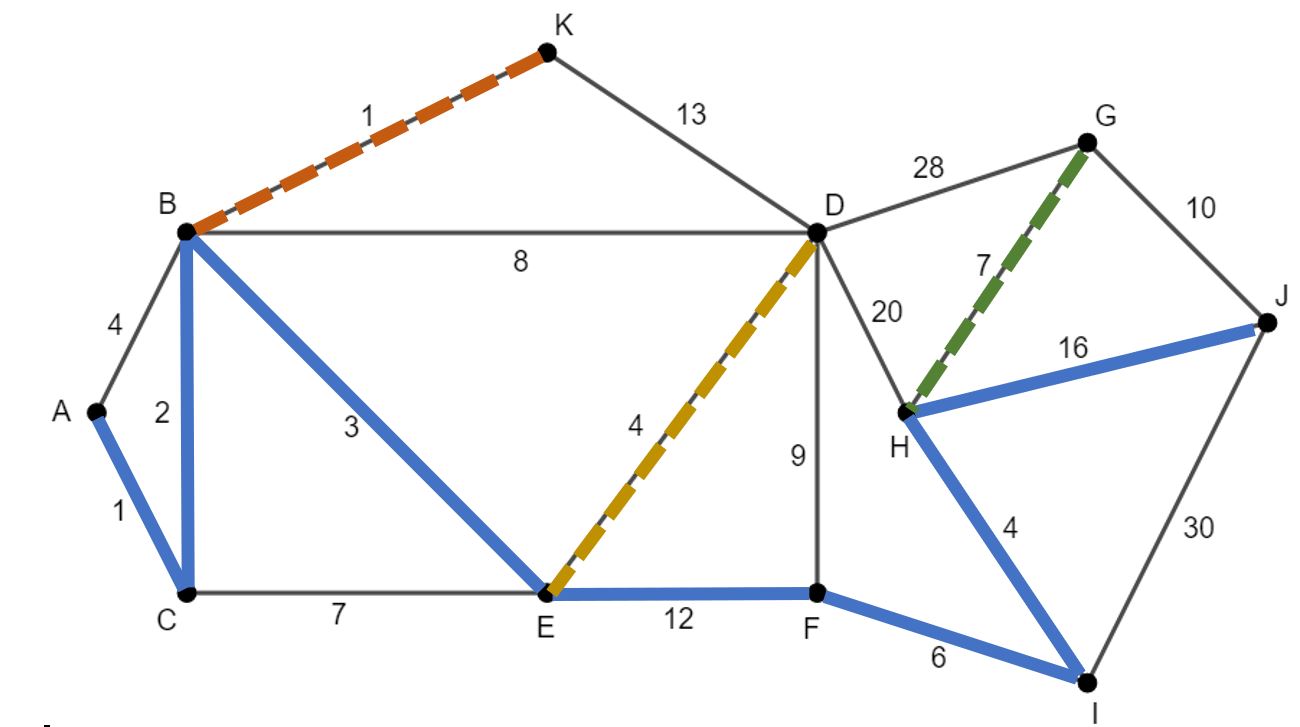
Pas nu het algoritme van Dijkstra toe op de graaf hieronder. Zoek de kortste route van \(A\) naar alle andere knopen.

 

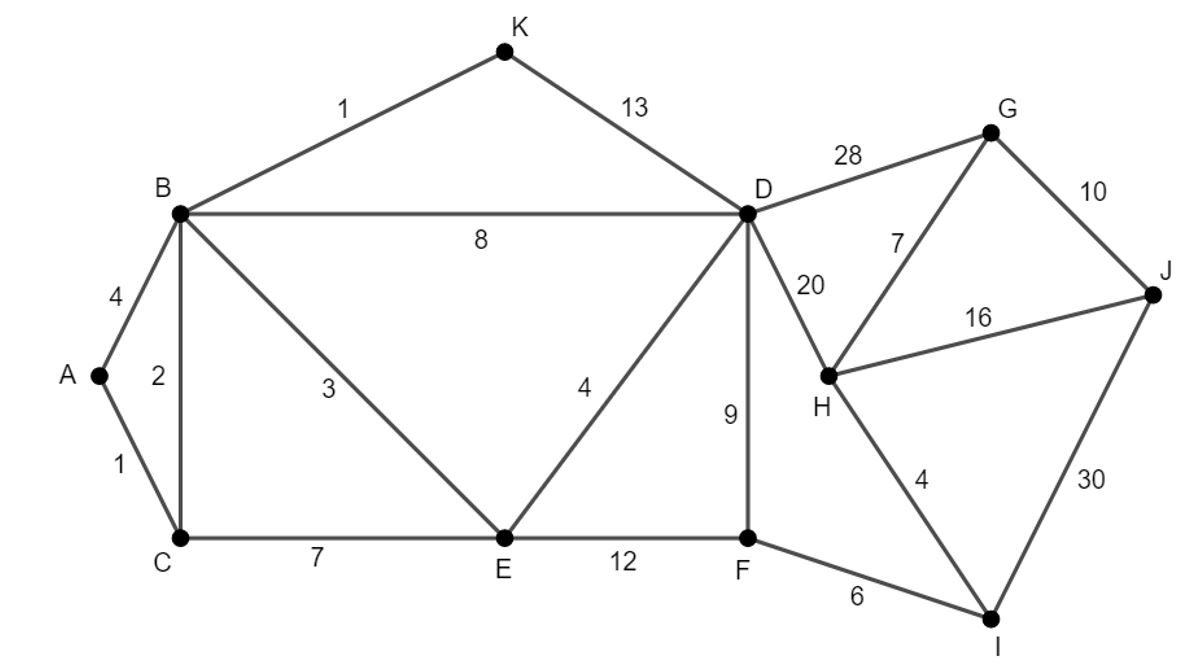
In plaats van de kandidaat-afstanden en ”van waar afkomstig” in te vullen in de graaf zelf, waarbij je de vorige waarden moet aanpassen, hou je alles bij in een overzichtelijke tabel. De eerste twee lijnen zijn al ingevuld. Vergeet niet om, nadat de tabel helemaal ingevuld is, de gevraagde kortste paden te geven. Duid die aan op de figuur.

 

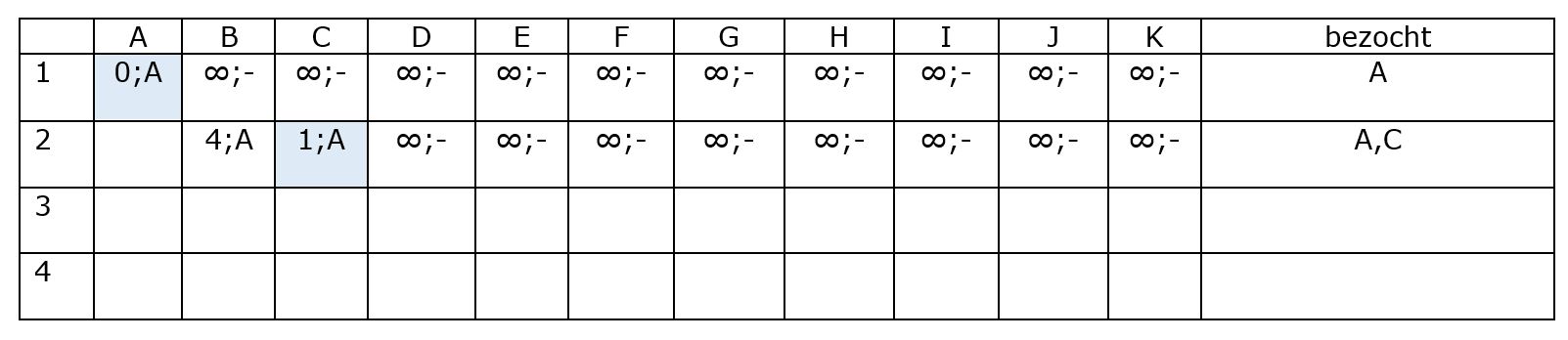
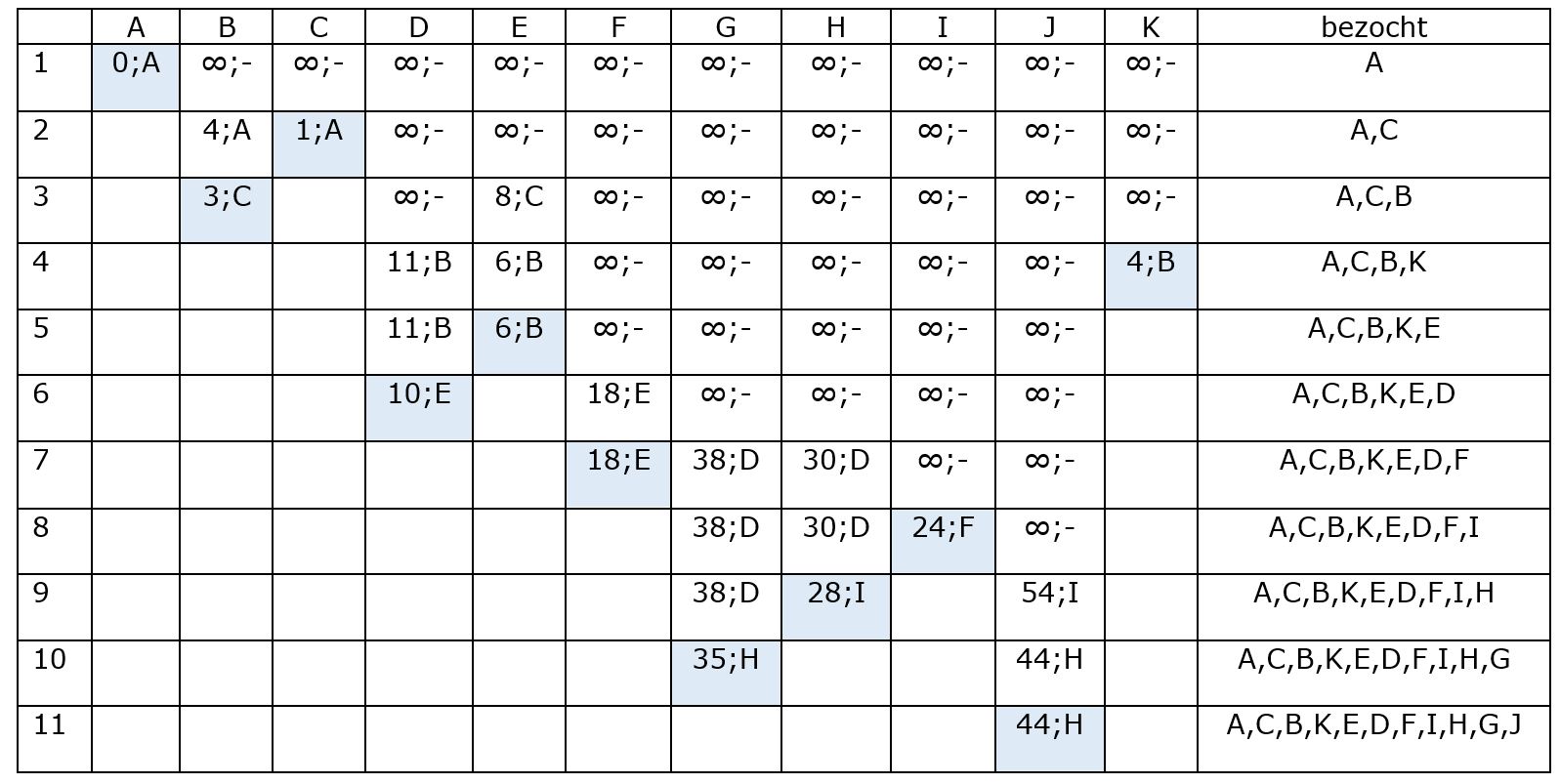
De ingevulde tabel vind je hieronder.

In de kolom van \(J\) zien we dat de kortste route afkomstig is van knoop \(H\). In de kolom van \(H\) zien we dat de vorige knoop \(I\) is. Enzovoort, tot we in de beginknoop \(A\) komen. Het kortste pad van \(A\) naar \(J\) is \(ACBEFIHJ\).

Analoog kun je uit dezelfde tabel het kortste pad aflezen van \(A\) naar elke andere knoop.

 

 

Dijkstra met een app

Op de site Graph Online (2015-2021) kun je de oplossing altijd controleren. Hoe werkt dit? We laten dit zien voor het uitgewerkte voorbeeld.

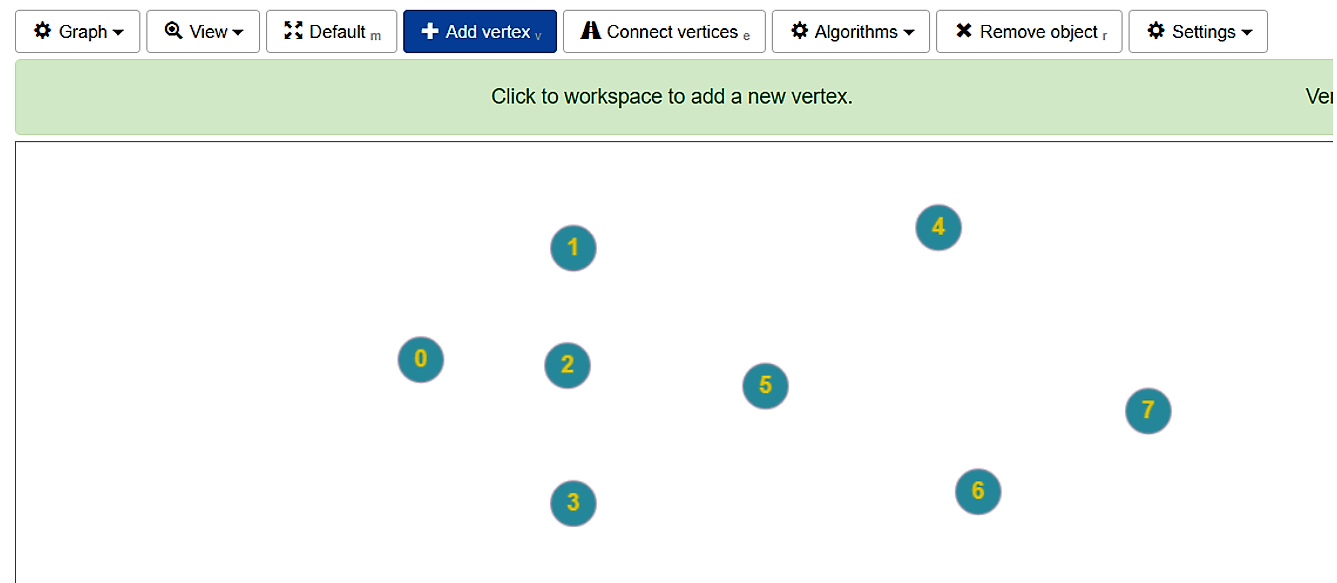
Figuur 16

 

Met ”add vertex’ kun je knopen maken door in het witte scherm te klikken (figuur 16).

Om knopen te verbinden met bogen, kies je ”connect vertices’. Dan klik je op de twee knopen die je wilt verbinden. Je krijgt het scherm van figuur 17 te zien.

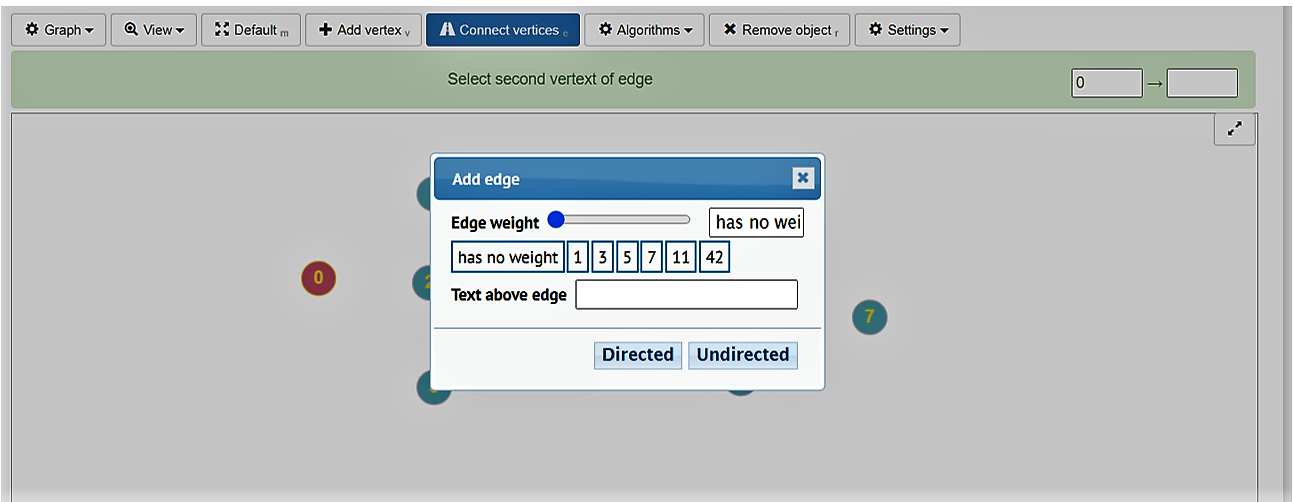
Figuur 17

 

Kies het gewicht van de boog. Klik op de knop ”undirected’. (Ongericht; er bestaan ook ”gerichte” grafen, met op de bogen pijltjes die je moet volgen zoals bij eenrichtingsstraten.) Dan krijg je het scherm van figuur 18.

Figuur 18

 

Zo maak je de graaf tot hij af is. Om een kortste pad te zoeken, klik je op ”algorithms”. Kies voor ”Find shortest path using Dijkstra’s algorithm’. Je kiest een startknoop en een eindknoop. De app geeft meteen aan welk pad het kortste is (figuur 19). Merk op dat deze app enkel de oplossing toont en niet de tussenstappen.

Figuur 19

 

 

Bronnen

[], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], [], []

Post a comment