1. Inleiding

De nieuwe eindtermen voor de tweede graad gingen in op 1 september 2021. Daarin werd ook een deeltje grafentheorie opgenomen voor de doorstroomfinaliteit. Er werd wel gestipuleerd dat dit onderwerp gerealiseerd dient te worden met een context.

In dit spinnenwebartikel bespreek ik daarom twee contexten om grafentheorie te behandelen, die ook werken voor leerlingen met minder uren wiskunde. Daarbij geef ik eerst, als echte wiskundige, een korte definitie van een graaf, en ga ik dan in op de twee boeiende contexten.

2. Enkele snelle definities

Ik zal het definitiegedeelte beperkt houden, te meer omdat eerdere artikels in Uitwiskeling het grafenconcept al duidelijk invoerden. Bijvoorbeeld het spinnenwebartikel Het kortstepad-algoritme van Dijkstra is interessant voor meer info.

Informeel gezien is een graaf een wiskundig model van een netwerk. Hieronder vind je een voorbeeld.

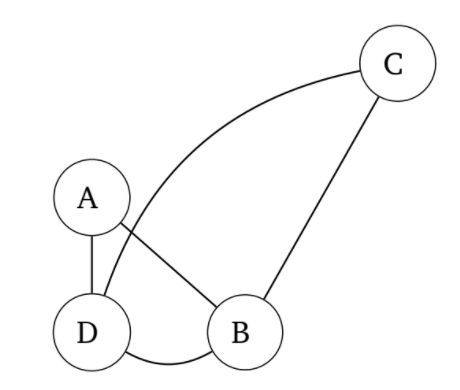
De knooppunten \(A, B,\ldots\) worden knopen genoemd, de verbindingen ertussen worden bogen genoemd. Merk daarbij op dat de locatie van de knopen er niet toe doet. Ook de vorm van de bogen doet er niet toe. Het enige dat telt bij een graaf, is welke knopen verbonden zijn.

In dit artikel gebruik ik echter gerichte grafen. De voorgaande figuur is een voorbeeld van een ongerichte graaf; bij een gerichte graaf hebben de bogen een richting. Die wordt vaak aangeduid met een pijltje, zoals hieronder te zien is.


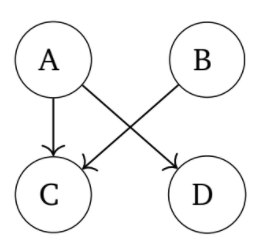
De gerichte graaf kan door sommigen als moeilijker beschouwd worden en bijgevolg minder geschikt voor klassen met minder uren wiskunde. In mijn ervaring vormde dit echter geen probleem en sloot deze wiskundige keuze dicht aan bij de te modelleren realiteit. Dat maakt het net doenbaarder voor de leerlingen.

3. Contexten voor grafen

In eerdere artikelen van Uitwiskeling werden reeds verschillende contexten aangeraakt. Bijvoorbeeld de loep Redeneren en puzzelen met grafen lijst er verschillende op, en ontwikkelt ook lesactiviteiten. Ook de loep Wiskunde rond besmettingsziekten is zeer interessant en linkt grafen aan de verspreiding van het coronavirus. Je vindt deze en andere interessante artikelen opgelijst bij mijn bronnen.

De onderstaande contexten zijn een interessante aanvulling bij de bestaande literatuur om volgende redenen. Het zijn ten eerste twee contexten die tot nog toe zelden effectief gebruikt werden in lessen, maar die wel heel dicht staan bij de leefwereld van de leerlingen. Ten tweede focus ik op vragen en lesactiviteiten die ook interessant zijn voor klassen met minder uren wiskunde, zonder te vervallen in het pure uitvoeren van algoritmes.

The Wiki Game

Laat ons dan de eerste context introduceren. Iedereen kent Wikipedia, de gratis open source encyclopedie. Enkele jaren geleden ontstond een online spel dat The Wiki Game genoemd wordt. Het spel kent vele varianten, maar ik beschrijf er hier één. In The Wiki Game worden twee willekeurige Wikipediapagina’s gekozen. Vervolgens moeten deelnemers met zo weinig mogelijk kliks van de ene naar de andere pagina doorklikken. Ze mogen enkel gebruik maken van de aanwezige hyperlinks op iedere pagina die ze passeren. Degene met het minste aantal kliks wint.

Deze context is interessant door het gaming-element dat veel leerlingen aanspreekt, de interactiviteit en competitie en het analyseren en bedenken van strategieën door wiskundig te reflecteren. Er is ook een actuele factor. Op televisie is er momenteel namelijk een segment in Iedereen Beroemd genaamd  Klikipedia, waarin teams The Wiki Game tegen elkaar spelen. Iedereen kan zich hiervoor inschrijven!

Hoe doe ik dit met mijn leerlingen?

Dit klinkt al leuk, maar je kunt het spel ook effectief met je klas spelen. Daarvoor maak je een groep aan op wikigam thewikigame.com en laat je je leerlingen inloggen op de website. Waarschuwing: leerlingen komen soms per ongeluk terecht op de wereldwijde Wiki Game. Dan spelen ze niet tegen hun klasgenoten, maar tegen willekeurige spelers van over heel de wereld. In je instructies voor je leerlingen moet je dus goed benadrukken op de rechterkant van het scherm de inlogcode in te geven. Je kunt daarbij ofwel willekeurige pagina’s als start en doel gebruiken, of zelfgekozen pagina’s.Je kiest zelf hoeveel rondes je speelt, hoe lang iedere ronde duurt en hoe je ze inkadert in je les. Je kunt leerlingen samen aan één computer zetten, zoals in Klikipedia, of elk apart. Een nadeel aan deze website is wel dat ze enkel in het Engels beschikbaar is.

Ik schets even het verloop van mijn les als inspiratie. Het gaat om een klas sociaal-technische wetenschappen in het vierde jaar. In het begin van de les was er redelijk wat tijd voorzien om iedereen technisch klaar te zetten. We speelden ook eerst een kennismakingsronde. Ik koos zelf op voorhand voldoende geschikte Wikipediapagina’s, waarvan ik wist dat een pad vinden tussen de twee doenbaar was. Na de kennismakingsronde speelden we een echte competitieronde, ronde 1. Na die ronde was er ruimte voor korte reflectie. Daarbij tekenden de leerlingen een schematische weergave van het pad dat zij genomen hadden en bespraken we ook klassikaal het kortst gevonden pad. De leerlingen konden ook openlijk strategieën bespreken.

Vervolgens speelden we ronde 2, die opnieuw opgevolgd werd met wiskundige reflectie. Deze keer werden de begrippen (gerichte) graaf, knoop en boog geïntroduceerd, die ze inoefenden aan de hand van hun getekende grafen.

De competitie en ook wiskundige analyse culmineerden in ronde 3. In ronde 1 ging het spel van België naar Britney Spears, in ronde 2 ging het spel van Lil Nas X naar België. Bij de derde ronde was er dus eerst een voorafgaande reflectie, waarbij de leerlingen de volgende vraag kregen: “Kun je puur met de grafen uit de vorige rondes iets besluiten over het aantal kliks om van Lil Nas X naar Britney Spears te geraken? Teken een graaf om je redenering te ondersteunen.” Deze vraag duidt op het aaneen kunnen plakken van gevonden paden. Ik had hiervoor met opzet deze pagina’s uitgekozen. Je kunt dus zeker van Lil Nas X naar Britney Spears gaan met een kleiner of gelijk aantal kliks als de som van het aantal kliks in de vorige rondes!

Verder wiskundig onderzoek

In dit spel bewandelen deelnemers eigenlijk een gerichte graaf. Daarbij zijn de knopen alle Wikipediapagina’s, en zijn de gerichte bogen de hyperlinks van één pagina naar een andere. In de les die ik hierboven beschreef, werden enkele begrippen ingevoerd en kwamen de leerlingen in aanraking met een driehoeksongelijkheid voor padlengte. Er kunnen extra wiskundige vragen gesteld worden die voor de snellere leerlingen interessant zijn. Ik lijst ze hier simpelweg op. Niet alle vragen zijn even bruikbaar als oefening, maar wel interessant als weetje.

Begin lesactiviteit

1. Bij The Wiki Game is een veelgebruikte strategie om eerst op de pagina Verenigde Staten te geraken. Deze pagina heeft namelijk heel veel links naar vele diverse onderwerpen. Stel deze strategie voor op een gerichte graaf

Hieronder vind je een voorbeeldantwoord.

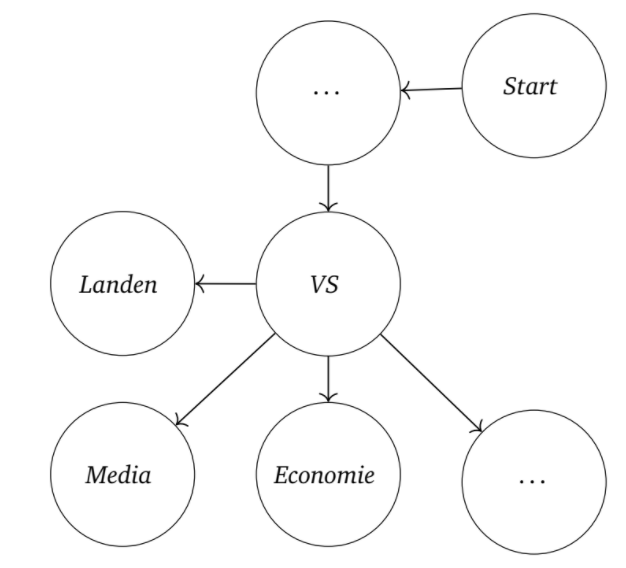
2. Laat zien dat er verschillende mogelijke paden zijn. Teken één gerichte graaf met twee verschillende paden tussen start- en doelpagina.}

Hier zie je een voorbeeldantwoord gebaseerd op sixdegreesofwikipedia.com.

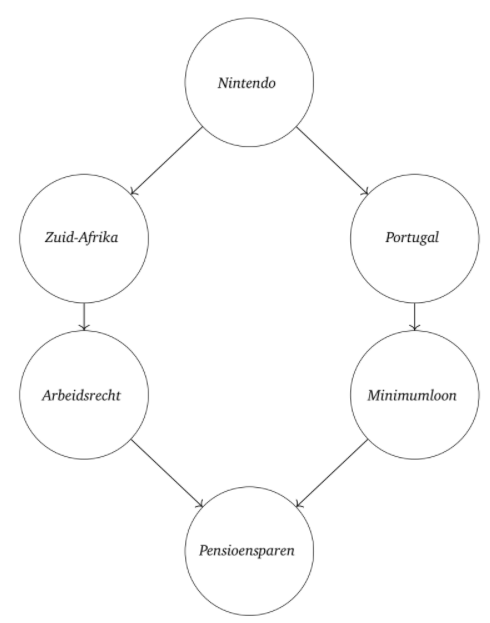
3. Wat gebeurt er op de graaf van Wikipediapagina’s en hun hyperlinks, als twee pagina’s samengevoegd worden?

Dan worden de twee knopen (Wikipediapagina’s) vervangen door één knoop die alle gerichte bogen overneemt van de twee originele knopen.

4. Vraagt het evenveel kliks om van pagina \(A\) naar pagina \(B\) te gaan als het omgekeerde (dus van \(B\) naar \(A\))? Verklaar!

Dit is niet noodzakelijk zo. Bij een gerichte graaf zoals het Wikipedianetwerk is het vinden van paden net inherent richtingsafhankelijk.

5. Is het mogelijk om vast te geraken tijdens het zoeken naar een pad? Is het met andere woorden mogelijk dat je niet weggeraakt van een bepaalde pagina?

Dit is effectief mogelijk. Ze hebben zelfs een aparte categorie binnen Wikipedia: Dead End pages.

6. Zijn er pagina’s die niet bereikbaar zijn tijdens dit spel?

Ja, ze vormen ook hun eigen categorie: Orphan pages. Voor zowel Dead End pages als Orphan pages wordt aan de vrijwilligers die Wikipedia opbouwen, gevraagd om ze te integreren in de rest van het netwerk. Er wordt dus actief ingezet op het zo klein mogelijk houden van deze categorieën. Dit maakt het moeilijk om een concreet voorbeeld te geven van een Dead End of Orphan, aangezien iedere nieuwe Wikipediapagina al snel ingebed zal zijn.

7. Is het mogelijk om vanuit iedere startpagina ieder andere pagina te bereiken?

Dit is een vraag naar de samenhangendheid van de graaf. Het bestaan van de bovenstaande categorieën toont aan dat Wikipedia niet samenhangend is.

Sociogram

Na deze extra wiskundige bedenkingen bespreek ik ook de tweede context voor grafentheorie. Sociale netwerken worden vaak als typisch voorbeeld genoemd van grafen. Ik maak hier concreter hoe je een sociogram (een graaf die een sociaal netwerk voorstelt) kunt gebruiken.

Sociogrammen worden op vele plaatsen gebruikt. Bedrijven zetten ze bijvoorbeeld in om een idee te krijgen van de werksfeer. Je kunt namelijk een sociogram opbouwen door iedere werknemer een simpele enquête te laten invullen. Dit is veel praktischer dan duizenden interviews te organiseren. Sometics is een voorbeeld van een website waar dergelijke visualisatiediensten aangeboden worden voor bedrijven. Niet alleen bedrijven maar ook leerkrachten kunnen sociogrammen gebruiken. Als je snel een nieuwe klas wilt leren kennen, stuur ze gewoon een enquête en je hebt onmiddellijk een idee van de klasdynamiek. De website Stoeltjesdans.nl bijvoorbeeld stelt op basis daarvan zelfs een stoelverdeling op. Sociogrammen worden ook gebruikt om een sociaal netwerk kwantitatiever te analyseren. Men kan bijvoorbeeld kwantificeren hoe geïsoleerd iemand is, of hoe populair iemand is, of er kliekjes zijn \( \ldots \)

Er zijn verschillende wiskundige modellen mogelijk van een sociaal netwerk. Van een gegeven groep kun je dus verschillende sociogrammen maken. Zo gebruikt Sometics bijvoorbeeld een gerichte, gewogen graaf. Het vriendennetwerk van Facebook is eerder een ongerichte, ongewogen graaf. Je kunt ook de knopen groter/kleiner voorstellen, afhankelijk van hoeveel vrienden de persoon heeft. Je krijgt dan een figuur zoals hieronder, waar populariteit heel snel uit af te lezen is.

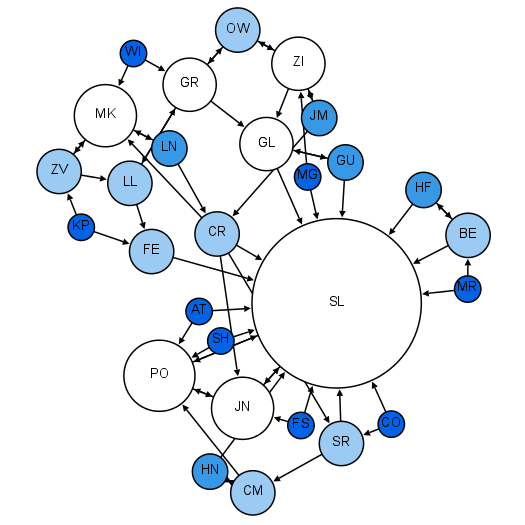
Wij houden het hier bij een gerichte graaf, net zoals bij de vorige context van The Wiki Game. De knopen zijn de mensen in de groep; de pijlen tussen de knopen betekenen ‘\( \ldots \) beschouwt \( \ldots \) als vriend’. Als twee personen elkaar als vrienden beschouwen, noteer ik dat met \(\longleftrightarrow\). Deze graaf wordt opgebouwd door een enquête te sturen naar de te bestuderen groep, waarbij gevraagd wordt jouw vrienden op te lijsten. Merk op dat in dit model vriendschap niet symmetrisch is.


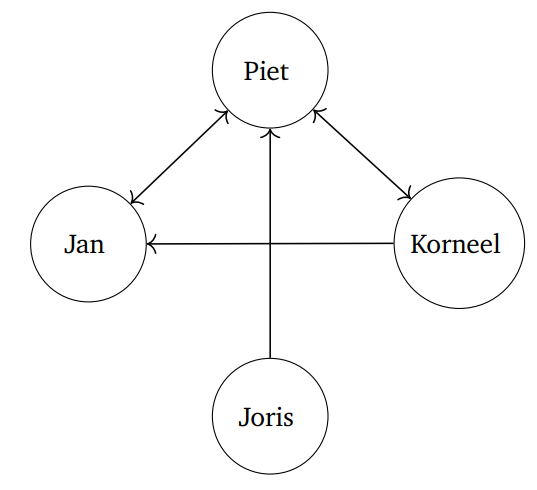
Deze context is een goeie keuze om grafen te introduceren, aangezien vriendschappen en populariteit een heel belangrijk iets is voor middelbare scholieren. Daarbovenop is het ook geschikt voor leerlingen met minder uren wiskunde, net omdat de context zo bekend is. De leerlingen in mijn klas hadden geen probleem met het gebruik van een gerichte graaf in plaats van een ongerichte. Wees je er wel van bewust dat het ook een mogelijks delicaat onderwerp is. Als je zelf niet veel vrienden hebt, kan het nogal confronterend zijn om een heel lesuur te spreken over ‘hoe geïsoleerd is deze persoon in de groep?’.

Hoe doe ik dat nu met mijn leerlingen?

In mijn eigen les behandelde ik sociogrammen na The Wiki Game. Je kunt zelf bepalen welke context (of een combinatie) meer gepast is voor jouw klas. De leerlingen kenden in mijn geval de begrippen graaf, knopen en bogen al.

De geschetste context was dat een leerkracht wilde weten hoe een fictieve klas in elkaar zat, en hij daarom een enquête had afgenomen. In de enquête moest iedere leerling zeggen wie hij/zij als vriend(in) beschouwde. De leerlingen kregen de lijst van (fictieve) antwoorden. Vervolgens moesten de leerlingen de data voorstellen als een gerichte graaf en zelf kiezen wat de knopen en bogen betekenden. Dit leverde (na enige klasdiscussie) het onderstaande sociogram op. Een pijl van \(A\) naar \(B\) betekent dus dat persoon \(A\) persoon \(B\) als vriend beschouwt.


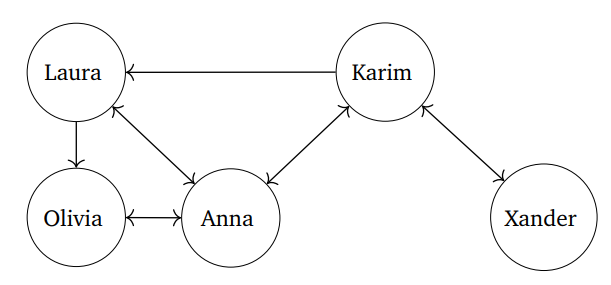
Vervolgens kregen de leerlingen verschillende vragen die de fictieve leerkracht zich ook zou stellen. Daarbij moesten ze telkens het sociogram gebruiken om hun antwoord te staven.

Begin lesactiviteit

1. Als er iets gebeurt met Olivia, zal Xander waarschijnlijk de laatste zijn die het te weten komt. Hoe zie je dit op het sociogram?

Olivia zal het aan haar vriendin vertellen, die het vervolgens aan haar vrienden verder zegt, enzovoort.  Aangezien Xander het meeste stappen verwijderd is van Olivia, zal hij het als laatste weten.   

2. Als je pesten wilt voorkomen, en je kunt één iemand kiezen om het goeie voorbeeld te stellen uit die klasgroep, wie zou je dan kiezen? Waarom die persoon?

Er zijn meerdere antwoorden en verklaringen mogelijk. Je kunt de persoon kiezen met de meeste pijltjes naar zich, of de persoon met de meeste pijltjes weg van zich. Je kunt ook iemand kiezen die gemiddeld gezien het minste aantal stappen verwijderd is van de anderen \( \ldots \)

3. Zijn er kliekjes in de klasgroep?

Het is één redelijke hechte groep, daarvan zijn de vele dubbele pijlen ook een teken.

Er zijn ongetwijfeld meer vragen te bedenken over het sociogram, maar dit bleef in mijn les beperkt aangezien de nadruk lag op The Wiki Game. Ik nodig je uit om zelf verdere vragen op te stellen. Het is ook een mogelijkheid om echte data te gebruiken voor het sociogram in plaats van fictieve antwoorden. Je kunt bijvoorbeeld de enquête naar een andere klas sturen. Anonimiteit van de antwoorden is dan wel uiterst belangrijk.

4. Conclusie

Dit spinnenwebartikel introduceerde twee contexten voor grafentheorie (aan leerlingen met minder uren wiskunde).Ik voorzag geen volledige werktekst, aangezien het slechts een kort artikel is, maar ook om je uit te nodigen het verder uit te zoeken. Deze twee contexten zijn interessant voor in de les, maar ook gewoon boeiend voor de wiskunde-enthousiasteling. Neem zeker eens een kijkje op thewikigame.com om The Wiki Game te verkennen en op Stoeltjesdans.nl om de mogelijkheden van sociogrammen uit te zoeken.

Bronnen

[], [], [], [], [], [], [], [], [], []

Post a comment