Absoluut van waarde

Martin Kindt

Euclides 97/5 (2022), 24-28

De artikels van Martin Kindt in Euclides zijn altijd interessant. Vaak starten ze met iets eenvoudigs, om verder via onvermoede verbanden en verrassende wendingen uit te monden in een stukje hogere wiskunde. In het maartnummer van Euclides heeft Martin het over de absolute waarde.

De absolute waarde van een reëel getal kun je op veel manieren definiëren, bijvoorbeeld meetkundig. De absolute waarde \(|a|\) van een reëel getal \(a\) is de afstand op de getallenlijn van dit getal tot het getal \(0\). Door te verschuiven leid je hieruit af dat de afstand tussen twee getallen \(a\) en \(b\) gelijk is aan hun ‘absolute verschil’ \(|a-b|\).

Grafieken met rechte stukjes

Met absolute waarden kun je functies maken waarvan de grafieken uit rechte stukken bestaan. Je komt die soms tegen in vragen van de wiskundeolympiade.

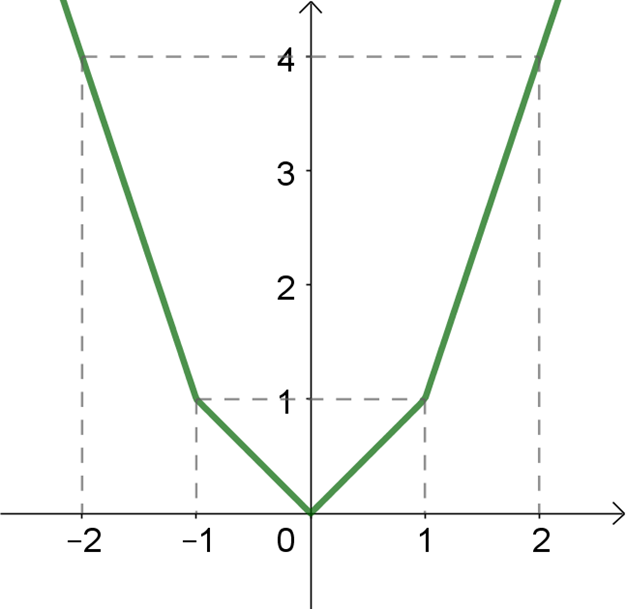
Een leerling tekent zijn eerste parabooltje met de lat in plaats van een vloeiende kromme (Figuur 1). Wat is het voorschrift van de getekende grafiek? Antwoord: \(x \mapsto |x|+|x-1|+|x+1|-2\).

Dit soort grafieken kun je ook met een mooie context introduceren. Martin citeert hiervoor uit eigen werk, een Hewet-boekje uit de jaren 1980.

Langs een rechte weg bevinden zich enkele torenflats \(A\), \(B\) … en er is geen andere bebouwing. Men wil een bushalte langs die weg plaatsen zodat de som van de afstanden tot die flatgebouwen minimaal is.

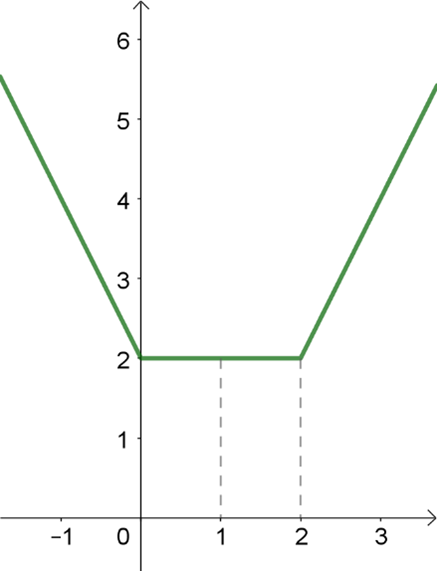
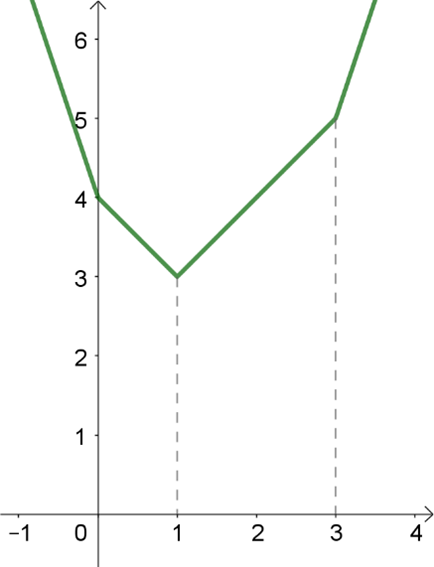
Beschouw de rechte weg als de \(x\)-as. De flatgebouwen worden dan getallen \(a, b\), … en het probleem leidt tot het bepalen van minima van functies \(x \mapsto |x-a|+|x-b|\) … In Figuur 2 en Figuur 3 zie je grafieken van dergelijke functies, voor twee en voor drie flatgebouwen.

Men kan aantonen dat in het algemeen voor een oneven aantal getallen \(a_1<a_2<…<a_{2n-1}\), het minimum van \(|x-a_1 |+|x-a_2 |+…+|x-a_{2n-1}|\) bereikt wordt bij de mediaan van die getallen, dus bij \(x=a_n\). Bij een even aantal getallen \(a_1<a_2<…<a_{2n}\) is er een heel interval van optimale waarden van \(x\), namelijk \([a_n,\;a_{n+1}]\).

Verrassend hoe de mediaan hier opduikt in een opgave die niets met statistiek te maken heeft! Je kunt in de opgave de som van de afstanden ook vervangen door de gemiddelde afstand; dan komen mediaan en rekenkundig gemiddelde samen in één opgave.

Ik neem me voor om dit probleem bij gelegenheid eens aan mijn leerlingen voor te leggen. Zouden ze, vertrekkend vanuit voorbeelden met twee, drie, vier en vijf flatgebouwen, tot deze algemene oplossing komen?

In hogere dimensies

Een mogelijk tweedimensionaal analogon voor de absolute waarde is de taxi-afstand. De absolute waarde van een koppel reële getallen \((x,y)\) is \(|(x,y)|=|x|+|y|\). Door te verschuiven, krijgen we de (taxi)afstand tussen twee punten \((x_1,y_1)\) en \((x_2,y_2)\) van het vlak: \(|x_1-x_2 |+|y_1-y_2|\). De punten die op afstand \(r\) van de oorsprong liggen vormen een vierkant (Figuur 4). Dit is dus een ‘taxicirkel’.

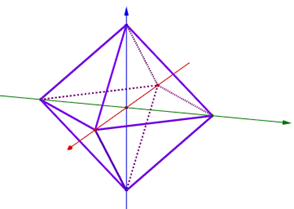
Een dimensie hoger vinden we de octaëder als ‘taxiboloppervlak’ (Figuur 5}). In de figuur zie je een draadmodel maar de vergelijking is die van het oppervlak van de octaëder (geen draadmodel, geen volle houten octaëder maar een kartonnen octaëder).

Hier houdt het niet mee op. In dimensie 4 stelt de vergelijking \(|x|+|y|+|z|+|t|=1\) een 16-cel voor, een van de zes regelmatige veelcellen in een vierdimensionale ruimte. Dit voorwerp heeft \(8\) hoekpunten (\(H=8\)), \(24\) ribben (\(R=24\)), \(32\) vlakken (\(V=32\)) en \(16\) octaëders als ‘cellen’, als 3D-zijlichamen (\(C=16\)). Het artikel rondt af met de veralgemening van de formule van Euler, \(H-R+V=2\), die we kennen van ‘bolachtige’ veelvlakken in de driedimensionale ruimte, tot andere dimensies:

• \(H=2\);
• \(H-R=0\);
• \(H-R+V=2\);
• \(H-R+V-C=0\).

Met wat combinatieleer en het binomium van Newton toont Martin aan dat de regelmaat (afwisselende tekens in het linkerlid; om beurten \(2\) en \(0\) in het rechterlid) zich wel degelijk verderzet in nog hogere dimensies. Waar een simpele absolute waarde toe kan leiden…

Michel Roelens