Inleiding
In het klassiek boek ”The Pythagorean Proposition’ verzamelde Elisha Scott Loomis (1852 – 1940) honderden bewijzen van de stelling van Pythagoras. Die gaan van simpele knip-en-plak-bewijzen tot bewijzen met vectorruimtes of zelfs quaternionen. Hij merkte daarbij op:
There are no trigonometric proofs, because: all the fundamental formulae of trigonometry, are themselves based upon the truth of the Pythagorean Theorem […]
Enkele maanden geleden vonden twee middelbare scholieren uit Amerika toch een goniometrisch bewijs voor de stelling van Pythagoras. In dit artikel onderzoeken we waarom dit zo verbazingwekkend is, zien we een reconstructie van hun nieuwe bewijs en reflecteren we even op het bewijs.
1. Is een ‘goniometrisch’ bewijs speciaal?
Opkomen met een goniometrisch bewijs van de stelling van Pythagoras is eigenlijk niet zo moeilijk. In het volgende kadertje toon ik er eentje van twee regels. De lezer merkt waarschijnlijk het probleem op, maar voor leerlingen kan dit een perfect aanvaardbaar bewijs lijken.
Het probleem is namelijk dat we de formule \sin^2 \alpha + \cos^2 \alpha = 1 gebruiken in de laatste gelijkheid, die typisch bewezen wordt met de stelling van Pythagoras. Het is dus wel degelijk een goniometrisch bewijs, maar een circulair. En dat is natuurlijk onaanvaardbaar.
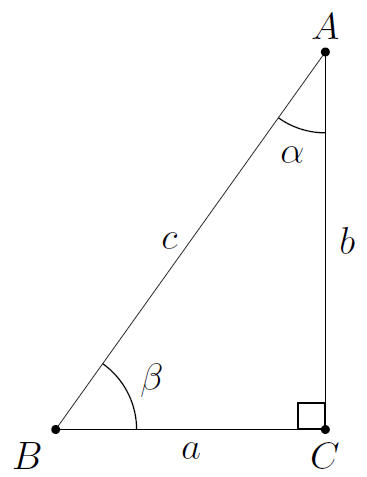
In de bovenstaande willekeurige rechthoekige driehoek is \sin \alpha = \frac{a}{c} en verder \cos \alpha = \frac{b}{c}. We isoleren daaruit a en b en maken een korte berekening.
a^2+b^2 = c^2\sin^2 \alpha + c^2\cos^2 \alpha = c^2
De laatste gelijkheid volgt uit de hoofdstelling van de goniometrie. Hiermee is de stelling van Pythagoras bewezen.
2. Het goniometrische bewijs
De twee scholieren, Ne’Kiya Jackson en Calcea Johnson (op de volgende foto), presenteerden hun goniometrische bewijs van de stelling van Pythagoras op een samenkomst van de American Mathematical Society. Ze hebben tot op heden nog niets gepubliceerd over hun vondst, en het is dus nog niet helemaal officieel. Op basis van verschillende foto’s uit hun presentatie en enkele nieuwsartikelen kon YouTuber MathTrain (zie bronnen) echter hun bewijs reconstrueren. Het is dus nog niet zeker dat dit hun effectieve bewijs is, maar het is desalniettemin een ideale leeropportuniteit.

Figuur 1 Afbeelding van Brett Duke (zie bronnen)
Het bewijs maakt gebruikt van de basisdefinitie van de sinus van een scherpe hoek, gelijkvormige driehoeken, de sinusregel en meetkundige reeksen. Het is dus iets te geavanceerd om aan te brengen als eerste contact met de stelling van Pythagoras, maar het kan wel terugkomen in één van de latere jaren (een aanrader als oefening op bewijzen en redeneren in de logicaleerlijn).
Je kiest als leerkracht natuurlijk zelf hoeveel je van dit artikel aan bod laat komen; je klas kan het bijvoorbeeld erg leuk vinden om meer achtergrond te weten te komen over de twee scholieren met een inleidende video; je kan ook onmiddellijk in de wiskunde vliegen met het schijnbewijs uit de inleiding; …
In de onderstaande lesactiviteit bouwen leerlingen (bedoeld voor derde graad) het volledige bewijs van Jackson en Johnson zelfstandig terug op.
Een goniometrisch bewijs van de stelling van Pythagoras
Jullie zagen jaren geleden een bewijs van de stelling van Pythagoras. Er zijn echter al heel veel bewijzen van die stelling gevonden. In 2023 werd nog een nieuw bewijs gevonden, door leerlingen net zoals jullie! Laten we het samen opnieuw opbouwen. We starten van de onderstaande driehoek \Delta ABC.

We bouwen nu eerst een grotere driehoek op, waarin we de stelling van Pythagoras zullen bewijzen.
- Spiegel \Delta ABC om [AC].Noem B’ het spiegelbeeld van punt B. Teken een rechte door B loodrecht op [AB]. Verleng [AB’] tot een rechte zodanig dat je het snijpunt D vindt van de twee rechten waarvan sprake is.
De tekening zou er nu als volgt moeten uitzien:
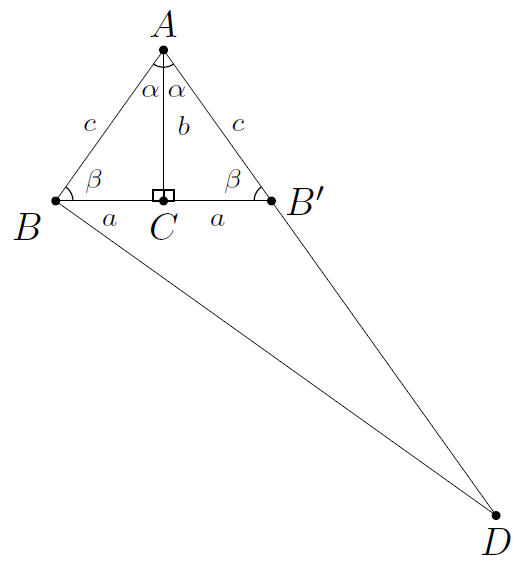
2. Laat B’ verticaal zakken tot lijnstuk [BD]. Noem dat punt dan B_1. Schuif B_1 horizontaal op naar lijnstuk [B’D].
Noem dat punt dan B’_1. Herhaal dit proces tot in het oneindige (in praktijk: 3 à 4 keer).
De tekening zou er nu als de onderstaande moeten uitzien.
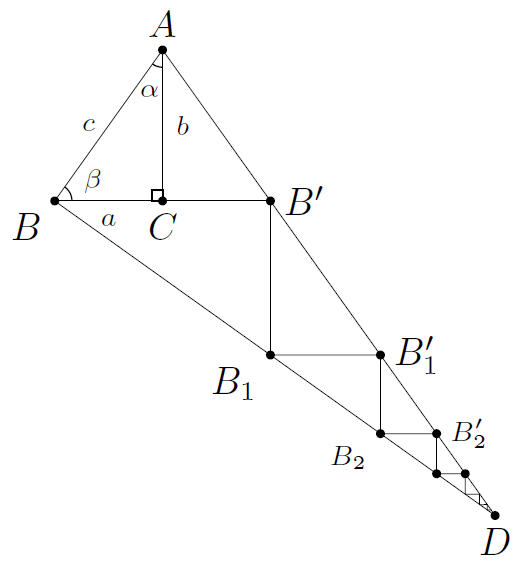
We kijken nu in detail naar deze figuur. Verderop, na de lesactiviteit, vind je een uitvergroot exemplaar met aangeduide afmetingen. We analyseren waar die vandaan komen.
3. Waarom is \widehat{DBB’}=\alpha? En wat betekent dat voor \widehat{B’B_1B}?
Per constructie staat [BD] loodrecht op [AB]. Uit \Delta ABC weten we dat \alpha en \beta complementaire hoeken zijn. Hieruit volgt onmiddellijk dat \widehat{DBB’} = \alpha. Aangezien \Delta BB_1B’ een rechthoekige driehoek is, volgt dan op gelijkaardige wijze dat \widehat{B’B_1B} = \beta.
4. Waarom is \widehat{B_1B’B’_1}=\alpha? En kun je deze argumentatie ook elders in de tekening toepassen, of is er iets uitzonderlijks aan deze hoek?
De hoeken in B’ moeten samen 180 graden vormen, aangezien ze aan een rechte grenzen. We weten al dat \widehat{AB’C}=\beta vanwege de spiegeling van \Delta ABC. Daarnaast is \widehat{BB’B_1}=90^{\circ} per constructie. Wegens complementariteit zoals voordien is dus \widehat{B_1B’B’_1}=\alpha.
Dit patroon zet zich ook verder.In de constructie teken je afwisselend horizontale en verticale lijnen, wat betekent dat bijvoorbeeld [B’B_1], [B’_1B_2], [B’_2B_3], \ldots allemaal evenwijdig zijn. Deze lijnstukken worden allemaal gesneden door lijnstuk [AD], waardoor de overeenkomstige hoeken gelijk zijn:
\alpha = \widehat{B_1B’B’_1} = \widehat{B_2B’_1B’_2} = \ldots
Een gelijkaardige redenering gaat op voor de horizontale lijnstukken in de constructie.
5. Is \Delta ABC gelijkvormig met \Delta BB_1B’? Zoja, geef de gelijkvormigheidsfactor in functie van de variabelen a, b en c. Wat leer je hierdoor over de zijden van \Delta BB_1B’?
Deze driehoeken zijn gelijkvormig, aangezien de hoeken overeenkomen. Om de gelijkvormigheidsfactor te bepalen kijken we naar lijnstuk [AC] en [BB’]. We starten in \Delta ABC met een lengte van b en krijgen een lengte van 2a in \Delta BB_1B’. De gelijkvormigheidsfactor is dus \frac{2a}{b}. Dit levert ook de lengtes \frac{2ac}{b} en \frac{2a^2}{b} op van de zijden van \Delta BB_1B’.
6. Op de tekening lijken alle driehoeken binnen \Delta BB’D gelijkvormig met \Delta BB_1B’. Klopt dit? Zoja, wat zijn de gelijkvormigheidsfactoren?
Ze zijn allemaal gelijkvormig wegens gelijke overeenstemmende hoeken. Kijken we naar \Delta BB_1B’ en \Delta B’B’_1B_1, dan is de gelijkvormigheidsfactor \frac{\frac{2a^2}{b}}{2a} = \frac{a}{b}, vanwege de overeenkomst tussen lijnstuk [BB’] en [B’B_1]. Kijken we naar \Delta B’B’_1B_1 en \Delta B_1B_2B’_1, dan is de gelijkvormigheidsfactor ook \frac{\frac{2a^3}{b^2}}{\frac{2a^2}{b}}=\frac{a}{b}, vanwege de overeenkomst tussen lijnstuk [B’B_1] en [B_1B’_1]. Dit patroon zet zich nu telkens verder: iedere overgang naar de volgende driehoek in \Delta BB’D betekent een vermenigvuldiging van de zijden met \frac{a}{b}.
7. Geef een driehoek die niet gelijkvormig is met de rest.
De grote driehoek DAB heeft hoekgroottes 2\alpha, 90^{\circ} en 90^{\circ}-2\alpha, en is dus niet gelijkvormig met de andere. Ook driehoek BB’D en BAB’ zijn niet gelijkvorming met de rest, om gelijkaardige redenen.
Nu hebben we dus een grote driehoek \Delta DAB die volledig bestaat uit oneindig veel gelijkvormige driehoeken.
Die driehoek zullen we gebruiken om de stelling van Pythagoras open te kraken.
8. Vind een uitdrukking in functie van a, b en c voor \sin{(2\alpha)} in \Delta BAB’. Hint: je kunt de sinusregel gebruiken.
Als je de sinusregel toepast in \Delta BAB’, krijg je
\frac{\sin{(2\alpha)}}{2a} = \frac{\sin{\beta}}{c}
\Leftrightarrow \sin{(2\alpha)} = \frac{2a\sin{\beta}}{c}
Je moet hierin nog \sin{\beta} vervangen door een uitdrukking in a, b en c. Die vind je in \Delta ABC, wat uiteindelijk de onderstaande gelijkheid oplevert.
\sin{(2\alpha)} = \frac{2ab}{c^2}
9. Vind een uitdrukking in functie van a, b en c voor |BD|. Vind ook zo’n uitdrukking voor |AD|.
De lengte |BD| is de som van een meetkundige rij met als eerste term \frac{2ac}{b} en met ratio \frac{a^2}{b^2}.
Dit betekent dat
|BD| = \frac{2ac}{b}\cdot \frac{1}{1-\frac{a^2}{b^2}} = \frac{c}{b^2-a^2}\cdot 2ab
Gelijkaardig is de lengte |AD| bijna de som van een meetkundige rij; er is één extra term.
|AD| = c + 2c\cdot \frac{a^2}{b^2} + 2c \cdot \frac{a^4}{b^4} + \ldots
= c + 2c\cdot \frac{a^2}{b^2}\cdot \frac{1}{1-\frac{a^2}{b^2}}
= \frac{c}{b^2-a^2}\cdot \left(a^2+b^2\right)
10. Vind een uitdrukking in functie van a, b en c voor \sin{(2\alpha)} in \Delta DAB. Hoe maak je nu het bewijs voor de stelling van Pythagoras af?
In driehoek \Delta DAB vinden we met de definitie van de sinus voor een scherpe hoek:
\sin{(2\alpha)}=\frac{|BD|}{|AD|}=\frac{2ab}{a^2+b^2}
Stellen we vervolgens de twee uitdrukkingen voor \sin{(2\alpha)} gelijk aan elkaar, dan vinden we
\frac{2ab}{a^2+b^2} \overset{\Delta DAB}{=} \sin{(2\alpha)} \overset{\Delta BAB’}{=} \frac{2ab}{c^2}
\Leftrightarrow a^2+b^2 = c^2
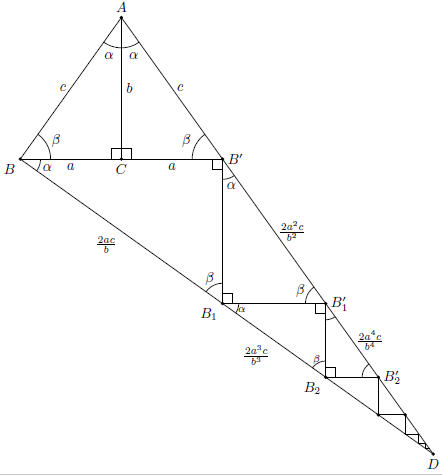
Figuur 2 De driehoek DAB met enkele afmetingen.
3. Klopt alles wel in het voorgaande?
3.1 Is het niet circulair?
In het vorige ingenieuze bewijs vonden Jackson en Johnson een (quasi-puur) goniometrische argumentatie voor de stelling van Pythagoras. Daarvoor gebruikten ze voornamelijk gelijkvormige driehoeken en puur de definitie van de sinus van een scherpe hoek. Daarnaast kwam eenmaal de sinusregel aan bod, en tweemaal de som van een meetkundige rij. Is hiermee het probleem van in de inleiding echter omzeild? Zijn we nu niet vervallen in circulair redeneren? We hebben nergens expliciet de formule \sin^2 \alpha + \cos^2 \alpha = 1 gebruikt, maar het kan alsnog zijn dat deze andere elementen eigenlijk afhangen van de waarheid van de stelling van Pythagoras. Welnu, de details hiervan worden hopelijk nog uitgespit in een aankomende publicatie van hen, maar we kunnen reeds enkele argumenten geven waarom geen circulariteit in dit bewijs zit.
Ten eerste kun je gelijkvormige driehoeken definiëren zonder de stelling van Pythagoras. Ten tweede heb je voor de definitie van de sinus als overstaande zijde gedeeld door schuine zijde enkel gelijkvormige driehoeken nodig, en dat is dus ook in orde. De sinusregel lijkt misschien het meest verdacht, maar ook deze heeft een bewijs dat los staat van de stelling van Pythagoras. Meer zelfs, online op Proofwiki (zie bronnen) vind je een bewijs dat enkel de definitie van de sinus van scherpe hoeken gebruikt. Tot slot is ook de formule voor de som van een meetkundige rij veroorloofd, aangezien dit volledig binnen de analyse opgebouwd en bewezen kan worden.
3.2 Zijn alle gevallen wel besproken?
Iets wat niet volledig is neergeschreven in de lesactiviteit, en wat een ideale uitdaging is voor je leerlingen, is de verhouding van \alpha en \beta. We moeten de stelling van Pythagoras voor alle rechthoekige driehoeken bewijzen. In de voorgaande tekeningen bekeken we enkel de situatie waar \alpha < \beta. Er moet dus nog eigenlijk iets gezegd worden over de situatie waarin \alpha > \beta en waar \alpha = \beta.
Als \alpha > \beta is er geen probleem. Je kunt simpelweg de driehoek omklappen zodat de kleinste hoek bovenaan staat, en alle zelfde stappen doorlopen. Eventueel kun je zelfs de namen (zoals \alpha en \beta) wisselen, zodat niets aan het bewijs verandert. Het grote probleem stelt zich wanneer \alpha = \beta. Indien \alpha = \beta, dan zijn beide hoeken gelijk aan 45^{\circ} en zijn ook beide rechthoekszijden gelijk. Op de figuur hieronder zie je dat er in dat geval geen snijpunt D bestaat, aangezien de twee rechten waar het om gaat parallel zijn.
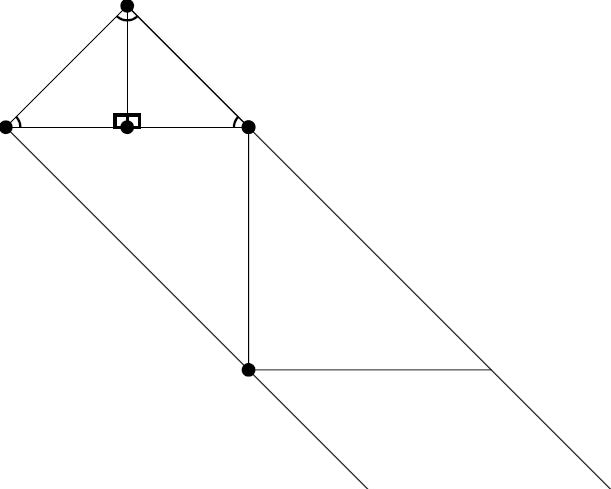
Hoe lossen we deze situatie nu op? Dit is een ideale bewijsoefening voor de leerlingen. Het is natuurlijk mogelijk om een klassiek knip-en-plak bewijs op te stellen zoals typisch wordt gedaan om de stelling van Pythagoras te bewijzen. Er bestaat echter een bewijs dat ietwat lijkt op dat van Jackson en Johnson, aangezien het gebruik maakt van de spiegeling van \Delta ABC en enkel de definitie van de sinus \ldots Op het einde van dit artikel toon ik dit bewijs.
3.3 Zijn we echt zeker dat het bewijs uit de inleiding niet werkt?
In de inleiding van dit artikel bekeken we een voorbeeld van een zogenaamd circulair bewijs van de stelling van Pythagoras. We namen daarvoor \sin^2 \alpha + \cos^2 \alpha = 1 aan, wat problematisch was aangezien die stelling typisch bewezen wordt met de stelling van Pythagoras. Het is echter niet omdat een stelling typisch gezien met de stelling van Pythagoras wordt bewezen, dat dat daarom de enige mogelijkheid is.
Conclusie
In dit artikel bespraken we een (gereconstrueerd) goniometrisch bewijs voor de stelling van Pythagoras. Dit is een ideale opportuniteit om leerlingen aan het bewijzen te krijgen; des te meer omdat de auteurs middelbare scholieren zijn. Het artikel eindigde met enkele toevoegingen over het bewijs, wat uitnodigt om (ook met leerlingen!) te reflecteren over de aard van bewijzen. Hieronder vind je nog een toevoeging aan het goniometrische bewijs van Jackson en Johnson voor gelijkbenige rechthoekige driehoeken.
In dit geval is \alpha = \beta = 45^{\circ} en ook a = b. Dit geeft ons de volgende figuur.
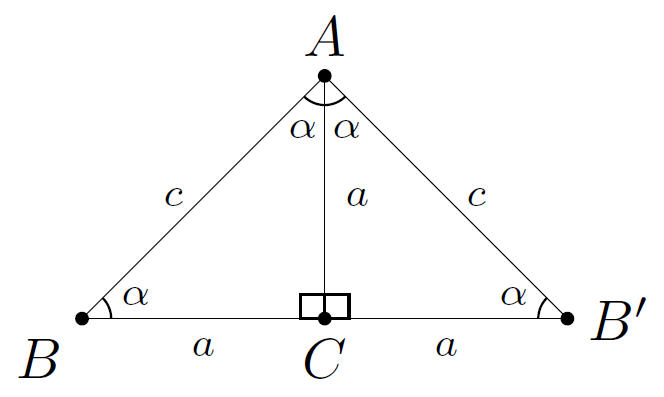
Je zou nu rechtstreeks de sinus van 45^{\circ} kunnen opzoeken in je goniometrische tabel, maar die waarde wordt echter typisch aangetoond met \ldots Je raadt het al: de stelling van Pythagoras. Om geen circulair bewijs uit te komen, kun je die dus niet gebruiken.
Je kunt \sin \alpha berekenen: één keer in \Delta ABC en één keer in \Delta BAB’. Dit geeft
\frac{a}{c} \overset{\Delta ABC}{=} \sin \alpha \overset{\Delta BAB’}{=} \frac{c}{2a}
\Leftrightarrow 2a^2 = c^2
\Leftrightarrow a^2 + a^2 = c^2
waarmee ook in dit geval de stelling van Pythagoras bewezen is.
Bronnen
- Bogomolny, A. (zd).\textit{ Trigonometric Proof of the Pythagorean Theorem.} Online. https://www.cut-the-knot.org/pythagoras/TrigProof.shtml
- Duke, B. (2023). St. Mary’s Academy seniors Ne’Kiya Jackson and Calcea Johnson are seen at the school in New Orleans. \textit{Nola}. https://www.nola.com/entertainment_life/st-marys-seniors-invited-to-atlanta-to-present-math-proof/article_292b0e3e-ce6a-11ed-b7df-33b7b9a2fbdf.html
- Jackson, N. \& Johnson, C. (2023). \textit{An Impossible Proof Of Pythagoras.} Conferentie American Mathematical Society Lente 2023. https://meetings.ams.org/math/spring2023se/meetingapp.cgi/Paper/23621
- Loomis, E. (1968). \textit{The Pythagorean Proposition.} National Council of Teachers of Mathematics. https://www.cosmoeconomics.com/EZ/ice/ice/SamplePages/sb_330_loomis_pythagorean-prop.pdf
- MathTrain. (2023). \textit{How High Schoolers Proved Pythagoras Using Just Trig! (and some other stuff).}YouTube. https://www.youtube.com/watch?v=nQD6lDwFmCc
- ProofWiki. (zd). \textit{Law of Sines.</h2> proofwiki.org. https://proofwiki.org/wiki/Law_of_Sines#Proof_1
- Vargas, R. (2023). US teens say they have new proof for 2,000-year-old mathematical theorem. \textit{The Guardian}. https://www.theguardian.com/us-news/2023/mar/24/new-orleans-pythagoras-theorem-trigonometry-prove
- Zimba, J. (2009). On the Possibility of Trigonometric Proofs of the Pythagorean Theorem. \textit{Forum Geometricorum. Volume 9, p275-278. https://scholar.googleusercontent.com/scholar?q=cache:Rp4zayuGq9wJ:scholar.google.com/+jason+zimba&hl=nl&as_sdt=0,5




 Onder de loep
Onder de loep