Een bijzondere tegel en een bijhorend wereldrecord

Periodieke betegelingen

Stel dat je een grote ruimte wilt betegelen met kleinere tegels, dan is dit beduidend makkelijker als je dat op een periodieke manier doet. Klassieke betegelingen met vierkanten, rechthoeken of zeshoeken hebben duidelijke rotatie-, spiegel- of translatiesymmetrieën. We noemen de achterliggende symmetriegroep een behangpapiergroep. Met wat groepentheorie kan men aantonen dat er maar 17 zulke groepen bestaan.

Aperiodieke betegelingen

Groot was dus de verbazing toen Roger Penrose in 1974 een betegeling vond met 2 vierhoekige tegels die tot in het oneindige verdergezet kon worden zonder ooit een symmetrie te hebben. Zou zulke aperiodieke betegeling ook mogelijk zijn met slechts 1 soort tegel? De zoektocht naar de aperiodieke monotegel of ein-stein was geopend.

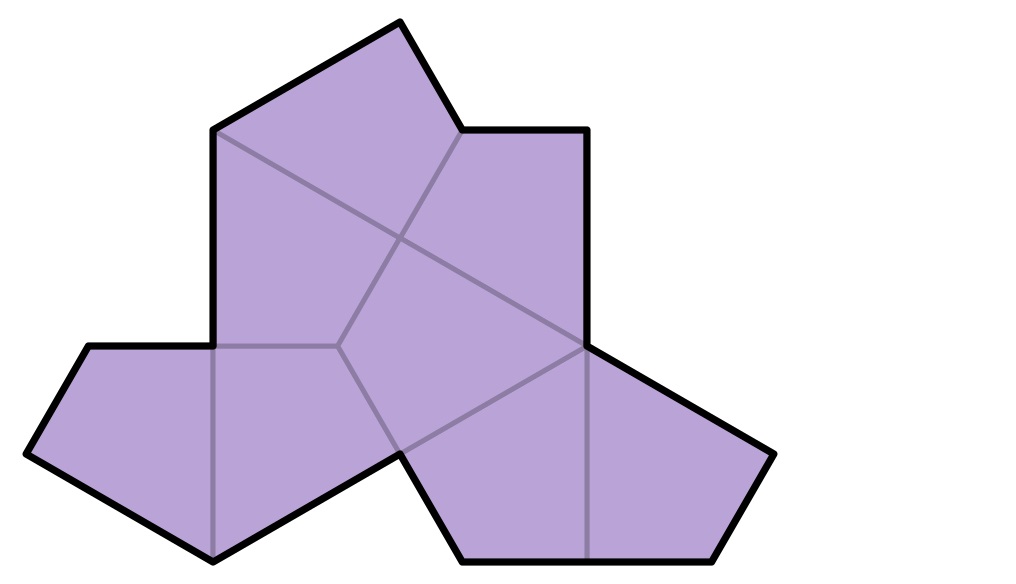
De aperiodieke monotegel of ein-stein

In maart 2023 werd het vermoeden bevestigd: aperiodiek betegelen is ook mogelijk met slechts 1 soort tegel. De dertienhoek hierboven werd voor het eerst ontdekt door David Smith, geen wiskundige, maar een kunstenaar! Smith contacteerde na zijn eerste bevindingen enkele wiskundigen die ook effectief konden bewijzen dat het hier om een ein-stein ging.

Het wereldrecord

Op 17 september 2023 vond in Brugge MathFest plaats waarbij de Imaginary tentoonstelling een feestelijk einde kende. Op deze dag kreeg de ein-stein ook een Belgisch kantje. Een groep enthousiaste puzzelaars slaagde erin om met maar liefst 6250 van deze tegels een (grote) vlakke figuur te vormen, geen sinecure voor een betegeling die aperiodiek en dus onvoorspelbaar is!

Bronnen

• Bollebus. Aperiodiek betegelen: een wereldrecord. https://bollebus.be/blog/wereldrecord-aperiodiek-betegelen
• Glaeser, G. en Polthier, K. Wiskunde in beeld. Uitgeverij Veen Magazines BV. p.174-182
• Smith, D. et al. An aperiodic monotile. https://arxiv.org/abs/2303.10798