Ik ben Frederik, wiskundeleerkracht op De Wingerd, een middelbare Freinetschool in Gent. Onze school behoort tot het OVSG, het net van de stedelijke en gemeentelijke scholen. Tot voor de vernieuwing had het OVSG eigen leerplannen. Op deze leerplannen waren de formules van Simpson duidelijk vermeld: leerlingen moesten ze kennen en ook kunnen toepassen.

Sinds de modernisering heeft OVSG voor de tweede en derde graad geen eigen leerplannen meer. Op hun website wordt duidelijk verwezen naar de leerplannen van de andere netten (GO!, Katholiek Onderwijs Vlaanderen en Provinciaal Onderwijs Vlaanderen).

Bij de vernieuwde leerplannen van het GO! en die van het Provinciaal Onderwijs Vlaanderen is er geen sprake meer van de formules van Simpson. Bij het Katholiek Onderwijs lezen we bij het leerplan wiskunde (derde graad doorstroomfinaliteit) voor richtingen met 6 uur wiskunde bij LPD 22 dat leerlingen de som- en verschilformules en de formules voor de dubbele hoek moeten kunnen gebruiken. Als extra worden daar de formules van Simpson gesuggereerd. Tot slot geven we mee dat in het Wiskundeplan de formules van Simpson wel zijn opgenomen in het leerplan van de derde graad.

Ik heb als leerkracht wiskunde steeds gebruik gemaakt van deze formules om in het zesde jaar (6 uur wiskunde) te starten met de afgeleide van de sinusfunctie. Nu de formules van Simpson niet meer tot de te kennen onderwijsdoelen behoren, is het dus ook wel interessant om te gaan kijken hoe we de afgeleide van de sinusfunctie kunnen berekenen met andere gekende technieken.

Afgeleide van de sinusfunctie

Toen ik dit schooljaar dit bewijs nog gaf door gebruik te maken van de formules van Simpson, had een pientere leerling – Sarp genaamd – mij al laten weten dat er ook een ander bewijs bestond om de afgeleide van de sinus te berekenen. Het is altijd een verrijking wanneer leerlingen zelf iets aanreiken en zeker wanneer hij me zei dat hij reeds benieuwd was geweest naar de afgeleiden van goniometrische functies. We hadden in het vijfde jaar namelijk het begrip afgeleide enkel toegepast op rationale en irrationale functies. We overlopen hier een bewijs over de afgeleide van de sinusfunctie zonder gebruik te maken van de formules van Simpson.

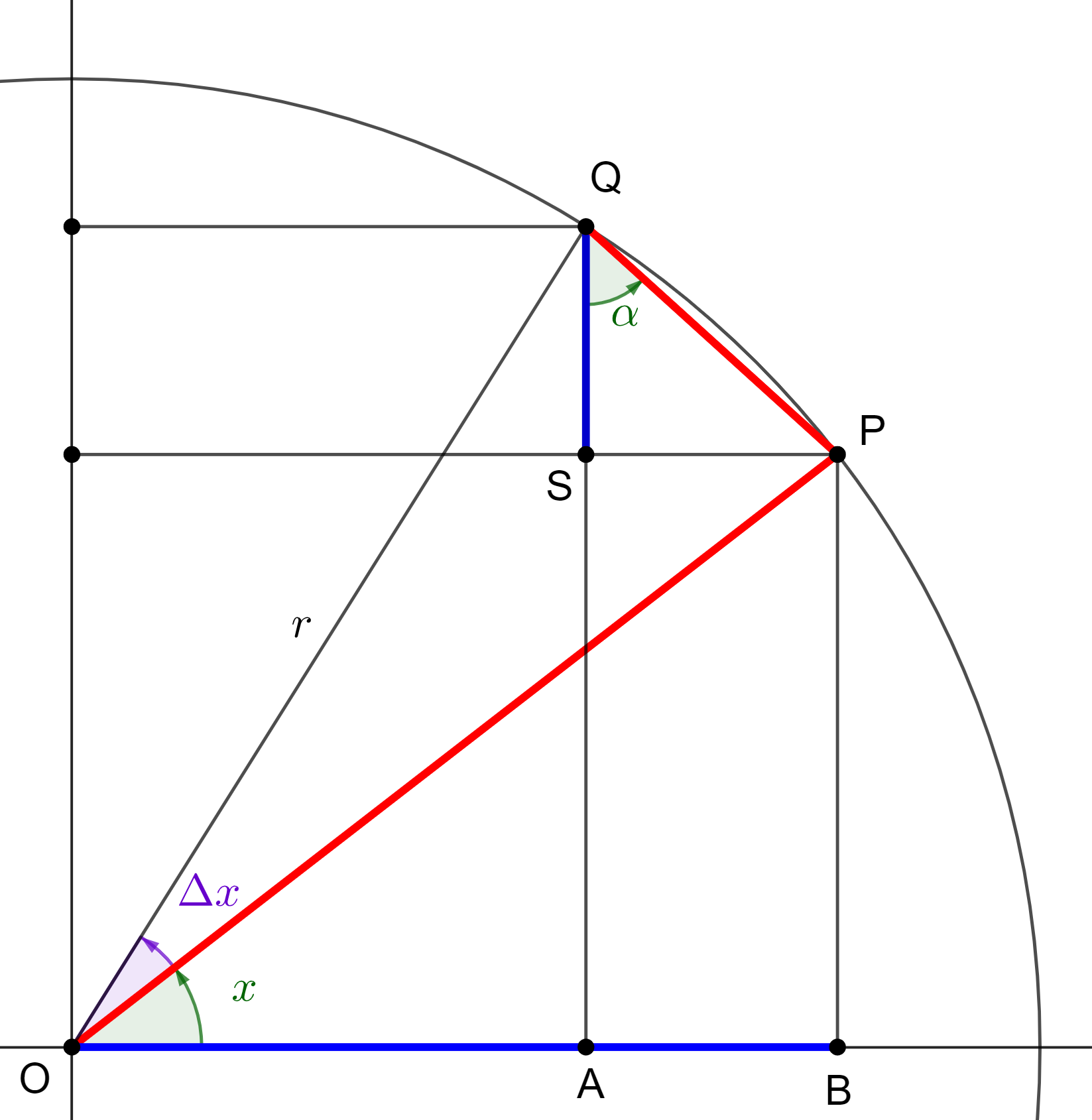
Figuur 1 Afgeleide bepalen via de goniometrische cirkel

 

In Figuur 1 is een cirkelboog getekend met een middelpuntshoek \(x\). We bekijken een toevoeging \(\Delta x\) van de hoekgrootte \(x\).

In de onderstaande redenering starten we bij de limietdefinitie van de afgeleide in een punt. In een volgende stap zullen we de sinussen bekijken als verhoudingen van de lengten van de zijden in bepaalde rechthoekige driehoeken, die duidelijk aangegeven zijn in Figuur 1.

We zien hier dat \(x\) een hoekgrootte is en dat \(\Delta x\) een verandering van deze hoekgrootte is. Cruciaal is ook dat de hoeken in radialen worden weergegeven. Alleen dan geldt de formule \(r \cdot \alpha\) voor de lengte van een cirkelboog met middelpuntshoek \(\alpha\) op een cirkel met straal \(r\).

De kerngedachte van dit bewijs is de gelijkheid van de lengte van het lijnstuk \(|PQ|\) en de lengte van de boog \(PQ\) als \(\Delta x\) naar nul gaat.

Bij de laatste stap hoort nog een woordje uitleg. De hoek \( \alpha \) zal naderen naar de hoek \(x\) wanneer \(\Delta x \to 0\). Dit wordt aangetoond door de loodrechte stand van de overeenkomstige benen van deze hoeken in de limietsituatie: \(OB \perp QS\) en \(OP \perp QP\). Als \(Q \to P\) wordt \(PQ\) een raaklijn aan de cirkel en die staat loodrecht op de rechte door dat raakpunt en het middelpunt van de cirkel.

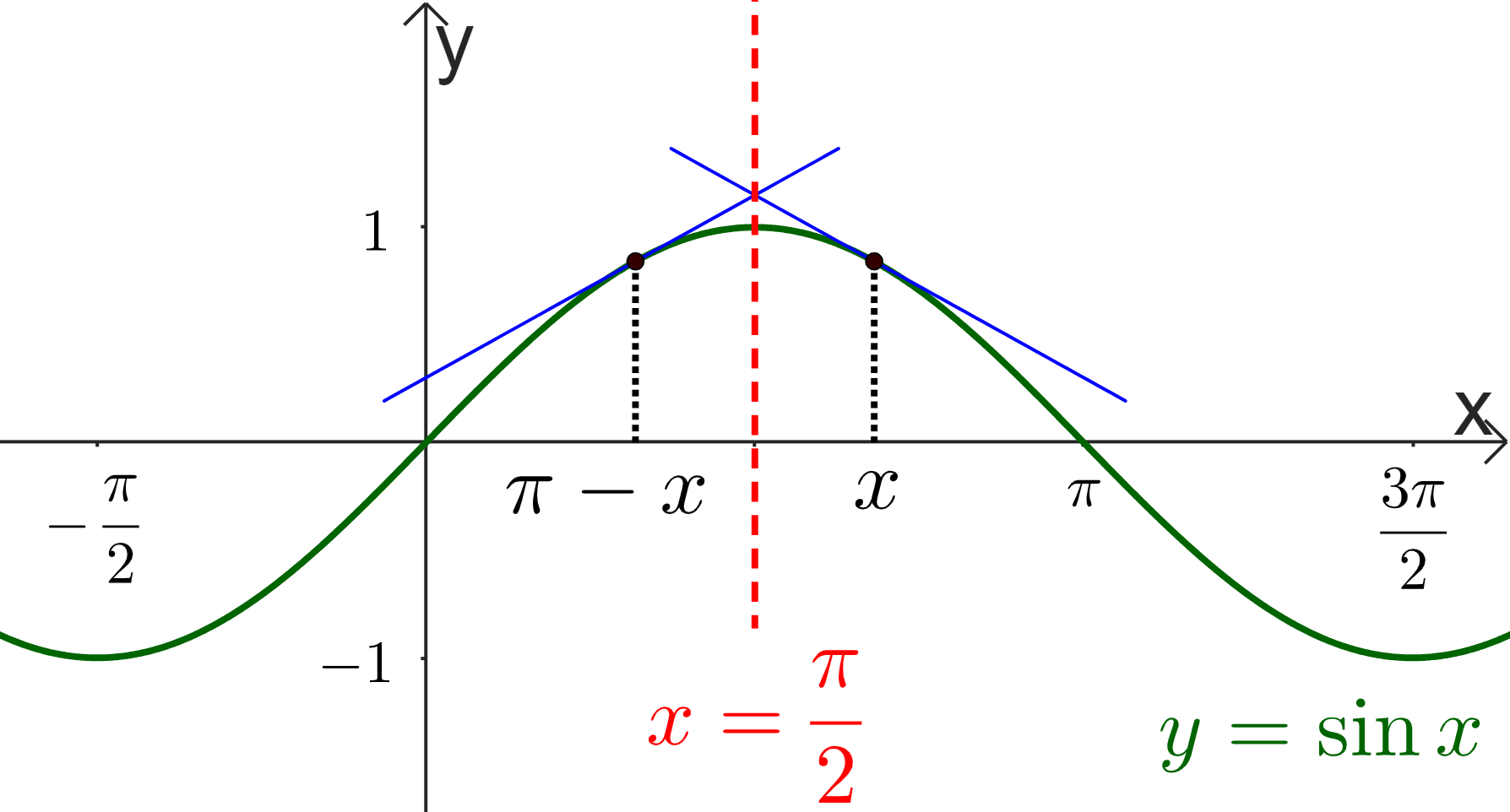
Figuur 2 Bewijs voor hoeken in het tweede kwadrant

 

Dit bewijs is enkel geldig voor hoeken in het eerste kwadrant. Voor hoeken in de drie andere kwadranten is er nog een bijkomende redenering nodig. We werken het bewijs hier uit voor hoeken in het tweede kwadrant.

Voor stompe hoeken zou dit bewijs bijvoorbeeld kunnen geleverd worden door de overgang naar de supplementaire hoek. De grafiek van de functie \(y=\sin x\) is symmetrisch rond de rechte met vergelijking \(x=\frac{\pi}{2}\), zie Figuur fig:tweedekwadrant}. De raaklijnen in de punten met \(x\)-coördinaat \(x\) en \(\pi-x\) hebben dus een tegengestelde richtingscoëfficiënt.

Voor hoeken \(x\) in het tweede kwadrant redeneren we dus als volgt:

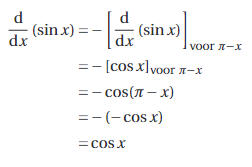
Voor hoeken die behoren tot het derde en vierde kwadrant kunnen we een analoge redenering maken. We geven dit mee als oefening.

Merk op dat in de opbouw van het bewijs hierboven de bijzondere limiet \(\displaystyle{\lim_{x \to +\infty}{\frac{\sin{x}}{x}}}\) niet meer voorkomt.

Het bewijs voor de afgeleide van de cosinusfunctie verloopt volledig analoog. Maar indien de kettingregel al gezien is, kun je je ook uit de slag trekken met de overgang van cosinus naar sinus door anticomplementaire hoeken. Wanneer we de sinusfunctie horizontaal over afstand \(\frac{\pi}{2}\) naar links verschuiven, verkrijgen we de cosinusfunctie.

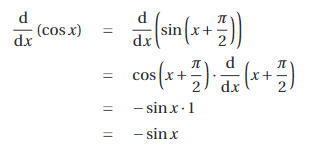
Zijn de regels van Simpson nu echt overbodig?

De formules van Simpson komen in de derde graad verschillende keren aan bod. In de eerste plaats voor het oplossen van goniometrische vergelijkingen. Een van de methodes steunt op het ontbinden in factoren en het toepassen van de eigenschap ‘product gelijk aan nul’. We illustreren dit met volgend voorbeeld.

Zo kan je de vergelijking \(\sin(5x)-\sin(3x)=0\) naast gebruik te maken van de formules van Simpson ook op een andere manier oplossen door \(\sin(3x)\) over te brengen en uit te drukken dat \(3x=5x+k2\pi\) of \(3x=\pi-5x+k2\pi\). Je zou op dezelfde oplossingsverzameling moeten uitkomen.

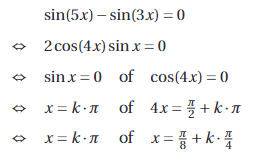
Hierbij is \(k\) een geheel getal. Deze methode is uiteraard zeer geschikt, maar bij eenvoudige vergelijkingen kan ze ook omzeild worden zodat er geen formules van Simpson aan te pas komen.

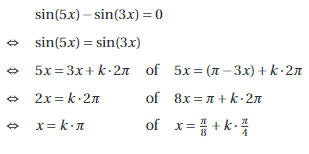
Beide oplossingentechnieken vragen ongeveer evenveel rekenwerk. Logischerwijs verkrijgen we dezelfde oplossingenverzameling. We stellen deze voor op de goniometrische cirkel in Figuur 2.

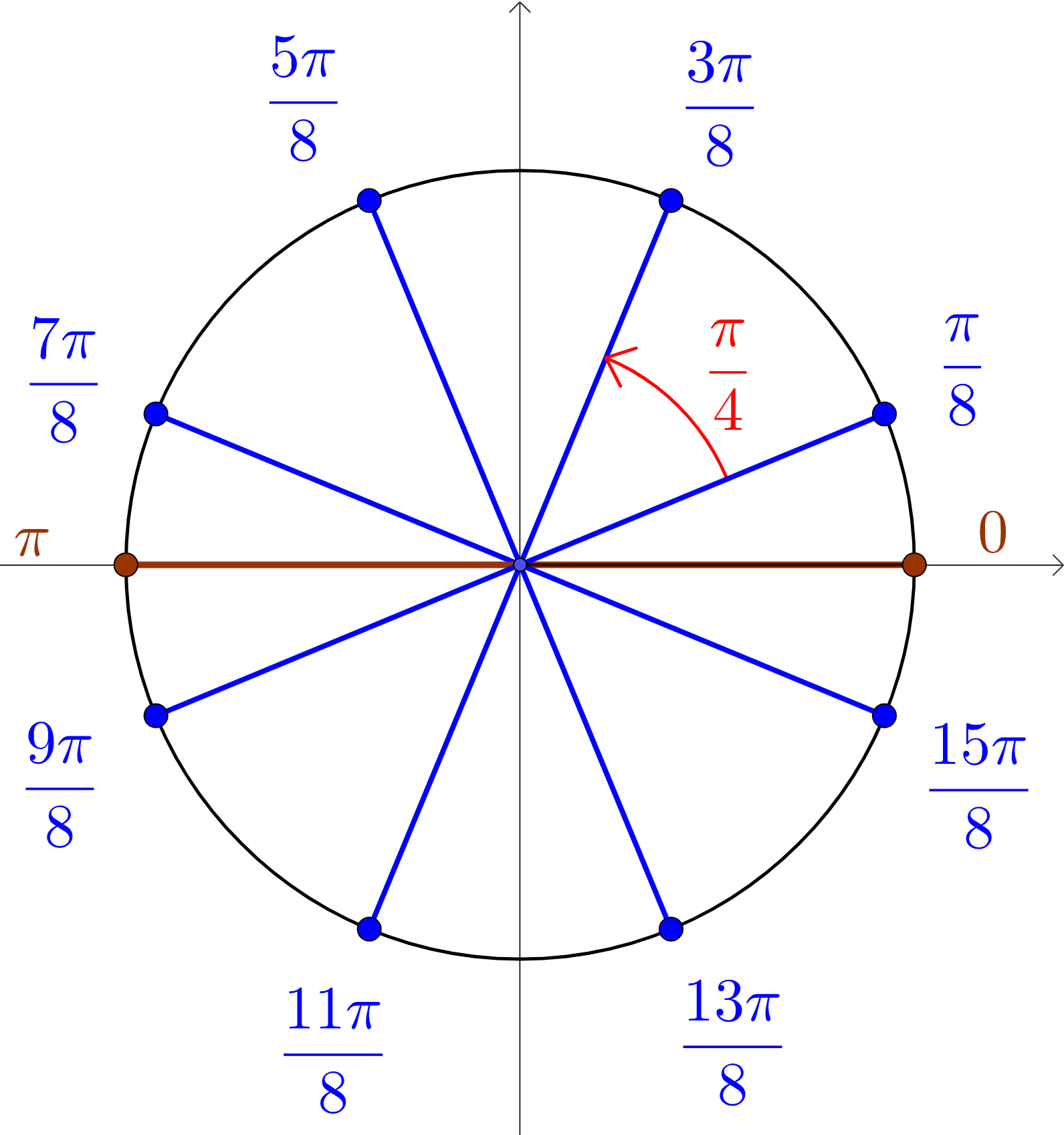
Figuur 2 Oplossingenverzameling

 

Het wordt moeilijker als we een term toevoegen aan het linkerlid. Een klassieke vergelijking uit handboeken van het vijfde jaar is:

\(\sin x+\sin(3x)+\sin(5x)=0.\)

Bij deze vergelijking kunnen we dit alternatief niet meer gebruiken en hebben we nood aan de formules van Simpson om tot een exacte oplossing te komen.

Een andere klassieker met de formules van Simpson is het vereenvoudigen van breuken met sommen van sinussen en cosinussen in de teller en de noemer. Hier zie ik geen sluipweg voor. Maar misschien is dit ook niet nodig als je er voor kiest je aan de minimumdoelstellingen te houden. Als je hier niet voor kiest, zijn de formules van Simpson een gemis.

Bij integraalrekening kunnen we gebruik maken van de omgekeerde formules van Simpson die ervoor kunnen zorgen dat we een product van sinussen en cosinussen kunnen herschrijven als een som, waardoor een integraal eenvoudiger te berekenen is. Zo kunnen we de integraal

\(\int\sin x\cos x \textrm{d}x\)

nog eenvoudig berekenen door gebruik te maken van de verdubbelingsformules, maar de integraal

\(\int\sin(5x)\cos(3x) \textrm{d}x\)

is niet zo eenvoudig te berekenen. Met de omgekeerde formule van Simpson

\(\sin(x)\cos(y)=\frac{1}{2}\left(\sin(x-y)+\sin(x+y)\right)\)

slagen we erin om deze integraal te herschrijven tot

\(\int\sin(5x)\cos(3x) \textrm{d}x = \frac{1}{2}\int\bigl(\sin(2x)+\sin(8x)\bigr) \textrm{d}x.\)

Deze laatste integraal is eenvoudig te berekenen door splitsing. Zelf heb ik nog geen toepassingen ontmoet buiten de wiskunde waar deze integraal in voorkomt. Vermoedelijk gaat het hier louter om een oefening binnen de wiskunde.

Wat denken de collega’s fysica hiervan?

In de fysica komen de formules van Simpson terug bij het samenstellen van trillingen. Een speciaal geval ontstaat als twee trillingen met ongeveer dezelfde frequentie optreden. Elk van deze trillingen wordt voorgesteld door een sinusfunctie. De toepassing vinden we vooral terug bij geluid en het stemmen van een gitaar of andere snaarinstrumenten. Indien de frequenties van deze twee tonen niet hetzelfde zijn, dan horen we zwevingen.

We proberen dit te illustreren met een eenvoudig voorbeeld. We beschouwen twee harmonische trillingen met dezelfde amplitude \(A=1\) en met respectievelijk frequentie \(f_1\) en \(f_2\):

\(\begin{align*}
y_1(t)= \sin\left(2 \pi f_1 t\right) \\
y_2(t)= \sin\left(2 \pi f_2 t\right)
\end{align*}\)

Wanneer we de som van deze twee harmonische trillingen nemen kunnen we gebruik maken van de formules van Simpson. We verkrijgen:

\(\begin{align*}
y_1(t)+y_2(t)
&= \sin\left(2 \pi f_1 t\right) + \sin\left(2 \pi f_2 t\right) \\
&=2 \sin \left({\frac{2 \pi \left(f_1+f_2\right)}{2}} t \right) \cos\left({\frac{2 \pi \left(f_1-f_2\right)}{2}} t \right) \\
&=2 \sin \biggl(\pi \left(f_1+f_2\right) \cdot t \biggr) \cos\biggl(\pi \left(f_1-f_2\right) \cdot t\biggr)
\end{align*}\)

We verkrijgen nu het product van twee periodieke functies waarvan de perioden respectievelijk gelijk zijn aan:

\(\begin{align*}
p_1 =\frac{2\pi}{\pi \left(f_1+f_2 \right)} =\frac{2}{f_1+f_2} \\
p_2 =\frac{2\pi}{\pi \left(f_1-f_2 \right)} =\frac{2}{f_1-f_2}
\end{align*}\)

Wanneer het verschil tussen de frequenties \(f_1\) en \(f_2\) kleiner wordt, zien we dat \(p_2\) groter wordt. We illustreren dit met drie gevallen, waarbij \(f_1=440Hz\) en \(f_2\) zal variëren. We geven even mee dat we de schaling van de assen niet veranderd hebben.

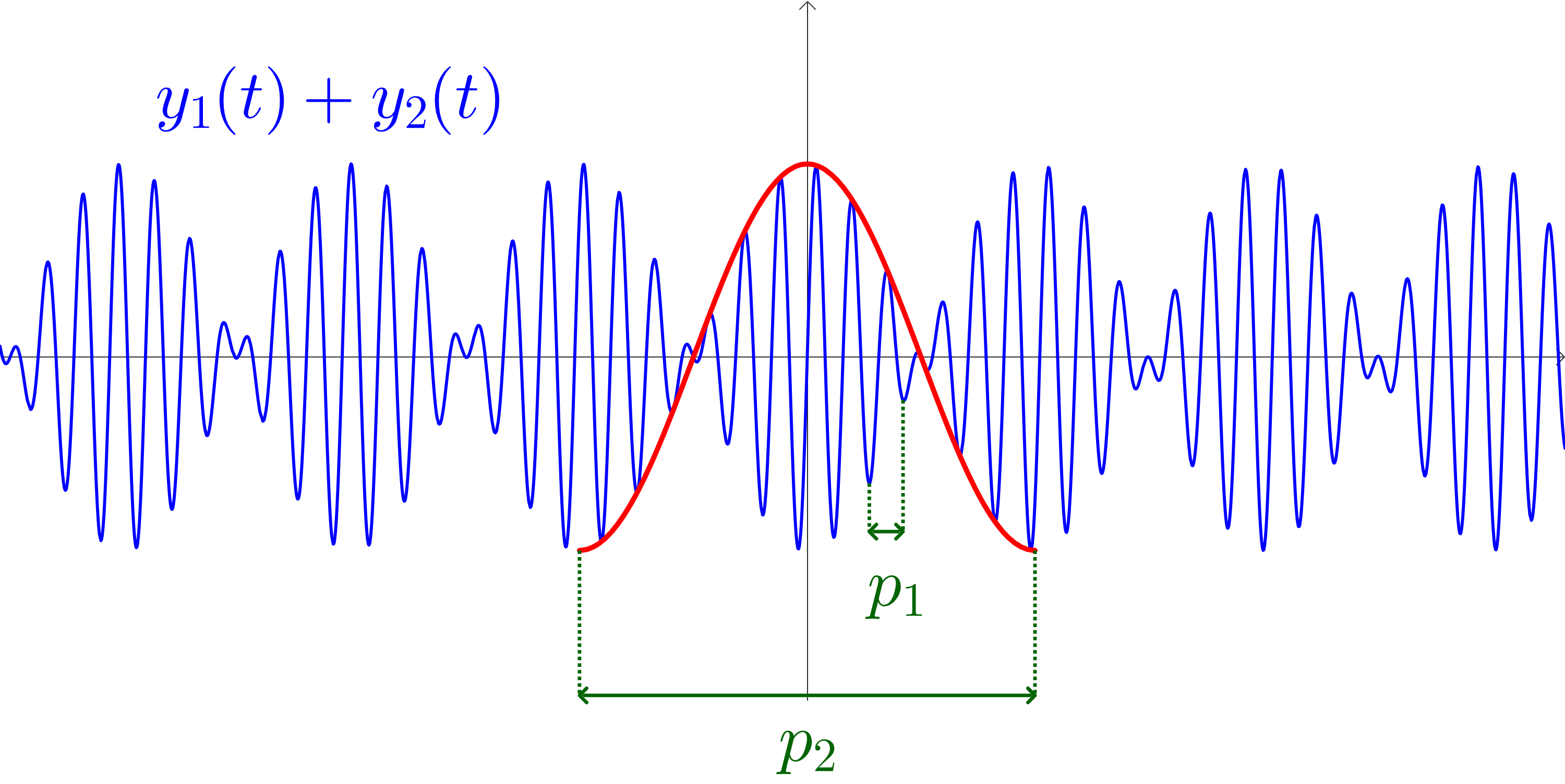
Figuur 3 f = 515Hz, het frequentieverschil is 75Hz

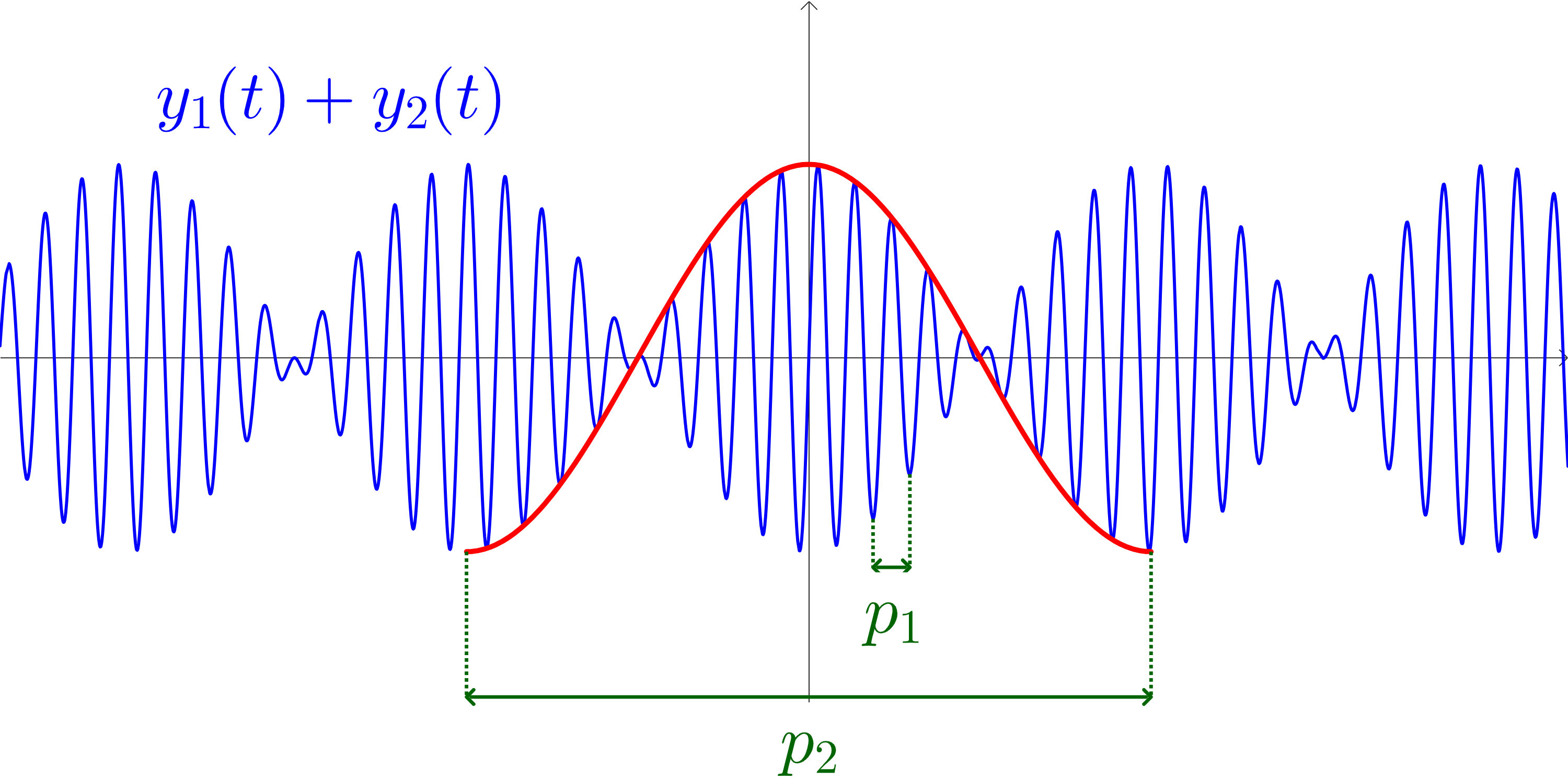
Figuur 4 f = 490Hz, het frequentieverschil is 50Hz

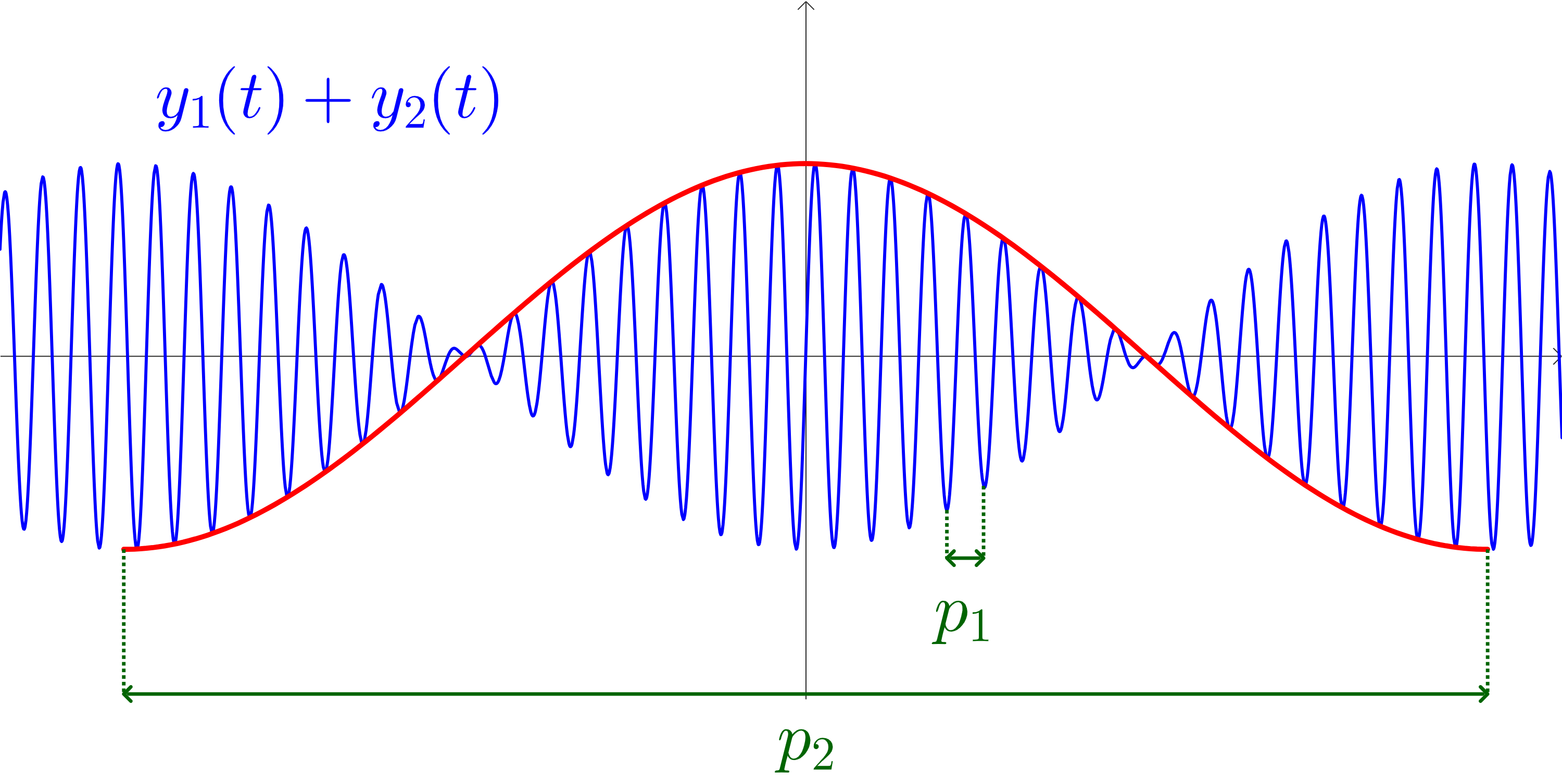
Figuur 5 f = 465Hz, het frequentieverschil is 25Hz

 

De rode omhullende grafiek met periode \(p_2\) accentueert dat de samengestelde toon regelmatige pulsen krijgt in de geluidsintensiteit. Bij geval drie zul je de samengestelde toon sterker en zwakker horen worden met een veel lagere frequentie (en een veel grotere periode) in vergelijking met geval 2 en geval 1. Dit noemen we zweven van een toon. Zwevende tonen duiden op een valse stemming.

We kunnen zwevingen makkelijk laten horen in de klas door middel van de grote stemvorken die in de fysicaklas te vinden zijn. Maar het is nog makkelijker ze te laten horen met de instructie PlaySound in GeoGebra. Hierover werd een spinnenwebbijdrage geschreven in Uitwiskeling 30/4.

Bij het stemmen van een gitaar zul je twee snaren tegelijk aanslaan en streef je ernaar om de frequenties \(f_1\) en \(f_2\) gelijk te krijgen. Storende zwevingen moeten dan vermeden worden. Maar in de klas, meerbepaald in de lessen wiskunde en fysica, mogen de zwevingen voor mij nog even blijven.

We verwijzen hier ook naar het filmpje Sinus plus sinus. Simpson met stemvorken, dat beschreven is in de loep Filmpjes in een wiskundeles (Uitwiskeling 26/2).

Bronnen

[], [], [], [], [], [], [], [], [], [], []

Post a comment