Er komt sleet op mijn lessen kansrekenen. Hoewel het voor mijn leerlingen elk jaar weer nieuw is als ze de tentvormige kansverdeling van een worp met twee dobbelstenen opstellen, ben ik zelf niet meer verrast. En ik straal ook geen verbazing meer uit als ik opmerk dat de kans om een 7 als ogensom te gooien zes keer groter is dan de kans om een 12 te gooien. Het is dus tijd om voor mezelf wat meer uitdaging en wat meer variatie te brengen in de les over de worp met twee dobbelstenen zonder de moeilijkheidsgraad voor de leerlingen te verhogen. Googelen was een eerste stap.
De dobbelstenen van Sicherman
Ik kwam al snel uit bij het dobbelstenenpaar van George Sicherman dat in 1978 door hem ontdekt werd. Het gaat om twee kubusvormige dobbelstenen die wat betreft ogenaantallen wel wat afwijken van de klassieke. Wat voornamelijk opvalt, is dat het aantal ogen verschilt tussen de twee dobbelstenen, dat bepaalde aantallen meer dan een keer voorkomen en dat de ogen per dobbelsteen geen rekenkundige rij meer vormen. Concreet, de ene dobbelsteen heeft ogenaantallen 1, 2, 2, 3, 3 en 4 en de andere heeft ogenaantallen 1, 3, 4, 5, 6 en 8. Het is mogelijk om de ogen zo op de beide dobbelstenen te plaatsen dat de som op tegenoverliggende zijvlakken bij de eerste steen gelijk aan 5 is en bij de tweede steen gelijk aan 9, maar voor wat volgt is dat niet van belang.
De laagste som die we met twee dobbelstenen van Sicherman kunnen gooien is 2 (1+1) en de hoogste is 12 (8+4). Het is niet moeilijk om in te zien dat de kansen op de laagste en op de hoogste worp gelijk zijn aan \frac{1}{36}. Maar het is niet evident om de andere kansen meteen goed in te schatten. Hiervoor moeten alle worpen met de twee ongewone dobbelstenen in kaart gebracht worden. Hieronder doen we dat voor het normale dobbelstenenpaar (N) en voor het paar van Sicherman (S).
In Figuur 1 zien we voor de worp met twee gewone dobbelstenen gelijke sommen op de rechten die evenwijdig lopen met de stijgende diagonaal van het vierkante diagram. De diagonaal van linksonder naar rechtsboven laat rechtstreeks zien waar de ogensom 7 is. Deze diagonaal telt zes hokjes. De kans op 7 is dus \frac{6}{36}. Even makkelijk kunnen we de kansen op 6 en op 8 aflezen. We voelen ook meteen aan dat de kansen gelijkmatig afnemen naar de uiterste worpen 2 en 12 toe.

Figuur 1 – Sommen van alle worpen met twee gewone dobbelstenen
Het overzicht in Figuur 2 ziet er heel wat chaotischer uit. De gelijke sommen, voorgesteld door gelijke kleuren, zijn nu niet meer te vinden op rechten evenwijdig met de stijgende diagonaal. De kansen op de verschillende worpen kunnen ook nu makkelijk uitgeteld worden maar het is niet meer evident om te zien dat er een gelijkmatige afname is van de kans op een 7 naar de kans op een 12 of naar de kans op een 2.

Figuur 2 – Sommen van alle worpen met twee dobbelstenen van Sicherman
Zeer onverwacht geven de twee dobbelstenen van Sicherman dezelfde kansverdeling als het gewone dobbelstenenpaar. Dit bracht me op een idee. Zouden er ook nog twee andere dobbelstenen bestaan, bijvoorbeeld in de vorm van een octaëder of van een dodecaëder, met een zelfde kansverdeling voor de ogensom als in Figuur 3? En kan deze kansverdeling ook voorkomen bij het werpen met drie of meer van deze ongebruikelijke dobbelstenen? Kunnen we gelijkaardige dobbelstenenduo’s of dobbelstenentrio’s vormen met negatieve getallen op de zijvlakken? En met breukvormige getallen? Op deze vragen hoop ik een antwoord te kunnen geven in dit spinnenwebartikel.
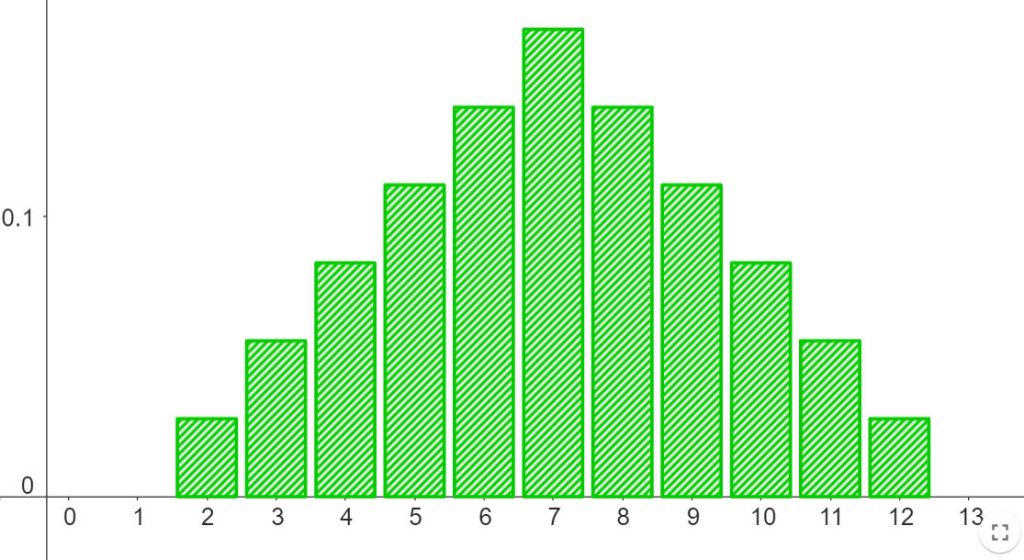
Figuur 3 – Het kansdiagram van de dobbelstenen van Sicherman
Bij een positief antwoord op de vragen hierboven hoop ik mijn leerlingen volgend jaar allemaal een ander stel kartonnen dobbelstenen te kunnen bezorgen waarover ik dan vragen stel zoals “Hoe groot is de kans om minstens een 10 te gooien als som van de ogen?”. Hoewel de dobbelstenen ogenschijnlijk random uitgedeeld zijn en ik de vragen willekeurig uit mijn mouw schud, zullen de antwoorden van de leerlingen toch gelijk blijken te zijn. Hoe cool is dit!
Een model voor het werpen met twee dobbelstenen
Een gekende modellering bij combinatorische problemen en bij kansproblemen is die met een <em>genererende functie}. Bij dobbelsteenproblemen kunnen we met een genererende veelterm werken waarop de ogenaantallen in de exponenten staan en het aantal mogelijkheden voor deze ogen in de coëfficiënten. Een dobbelsteen waarbij je 1 mogelijkheid hebt om 6 te gooien, 1 mogelijkheid om 5 te gooien, enz… kun je bijvoorbeeld modelleren met de veelterm:
1\cdot x^6+1\cdot x^5+1\cdot x^4+1\cdot x^3+1\cdot x^2+1\cdot x^1.
Waarom we een dobbelsteen modelleren door middel van een veelterm, blijkt meteen. Als we twee dobbelstenen samen opgooien en we nemen de som van de aantallen ogen die gegooid zijn, dan kunnen we het aantal mogelijkheden voor elke som vinden door de twee veeltermen geassocieerd met de twee dobbelstenen met elkaar te vermenigvuldigen. Stel bijvoorbeeld dat je twee gewone dobbelstenen samen opgooit, dan kun je de bijbehorende veelterm met zichzelf vermenigvuldigen:
(1\cdot x^6+1\cdot x^5+1\cdot x^4+1\cdot x^3+1\cdot x^2+1\cdot x^1)^2.
We krijgen nu een veelterm van graad 12. Dit getal is de hoogst mogelijk worp met twee dobbelstenen. Als je de term in x^5 in de uitwerking bepaalt dan zie je meteen hoeveel mogelijkheden er zijn om een 5 te krijgen als som van het aantal ogen:
1 \cdot 1 \cdot x^{1+4}+1 \cdot 1 \cdot x^{2+3}+1 \cdot 1 \cdot x^{3+2}+1 \cdot 1 \cdot x^{4+1}.
Dit levert de term 4x^5 op. Hieruit leid je af dat er 4 manieren zijn om een 5 te gooien met de twee gewone dobbelstenen.
Als we het kwadraat van deze zesdegraadsveelterm helemaal uitwerken
1 \cdot x^{12}+2 \cdot x^{11}+3 \cdot x^{10}+4 \cdot x^9 + \dots + 3 \cdot x^4 +2 \cdot x^3 +1 \cdot x^2
dan verschijnt de hele kansverdeling (op een factor \frac{1}{36} na) in de coëfficiënten van deze veelterm.
De verklaring voor deze modellering is dat de berekening die je doet met de ogenaantallen en de frequenties van de ogenaantallen precies dezelfde is als bij productberekening van de genererende veeltermfuncties. Je telt zowel de ogenaantallen op als de exponenten van de veeltermfuncties. En je vermenigvuldigt de frequenties van de ogenaantallen van de twee dobbelstenen maar eveneens de coëfficiënten van de veeltermfuncties.
Deze modellering lukt ook voor andere dobbelstenen, bijvoorbeeld die van Sicherman. De dobbelsteen met de grote aantallen op de zijvlakken wordt gemodelleerd als
1\cdot x^8+1\cdot x^6+1\cdot x^5+1\cdot x^4+1\cdot x^3+1\cdot x^1
en die met de kleine aantallen als
1\cdot x^4+2\cdot x^3+2\cdot x^2+1\cdot x^1.
Het product van deze twee veeltermen is ook gelijk aan
1 \cdot x^{12}+2 \cdot x^{11}+3 \cdot x^{10}+4 \cdot x^9 + \dots + 3 \cdot x^4 +2 \cdot x^3 +1 \cdot x^2.
Zo kunnen we op een alternatieve manier controleren dat het dobbelstenenpaar van Sicherman eenzelfde kansverdeling oplevert als gewone dobbelstenenparen.
Via de bovenstaande redenering lieten we zien dat de kansverdeling bij het werpen van meerdere dobbelstenen neerkomt op het vermenigvuldigen van veeltermen. Als je de kansverdeling van de worp met meerdere dobbelstenen echter al kent en je wil de kansverdeling van de afzonderlijke dobbelstenen achterhalen, dan hebben we de omgekeerde operatie nodig: ontbinden in factoren. Dit is de clou van de volgende paragraaf. En hiermee wordt ook een link gelegd naar de loep van Uitwiskeling 40/3.
Een alternatief voor de dobbelstenen van Sicherman
In de vorige paragraaf lieten we zien dat de kansverdeling voor de worp met twee gewone dobbelstenen gegeven wordt door de veelterm
(1\cdot x^6+1\cdot x^5+1\cdot x^4+1\cdot x^3+1\cdot x^2+1\cdot x^1)^2.
Mits wat handigheid kunnen we deze veelterm manueel ontbinden in factoren: eerst de factor x^2 afzonderen, daarna de termen drie aan drie samennemen, verder de som van twee derdemachten ontbinden.
(x^6+x^5+x^4+x^3+x^2+x^1)^2
=x^2(x^5+x^4+x^3+x^2+x+1)^2
=x^2 \left( x^3(x^2+x+1)+(x^2+x+1)\right)^2
=x^2 \left( (x^2+x+1)(x^3+1)\right)^2
=x^2 \left( (x^2+x+1)(x+1)(x^2-x+1)\right)^2
= x^2(x+1)^2(x^2+x+1)^2(x^2-x+1)^2.
Wie er geen uitdaging aan vindt om deze ontbinding manueel uit te voeren, kan ze natuurlijk ook overlaten aan een computerprogramma met algebraïsche capaciteiten (een CAS-programma).
Deze veelterm kunnen we op verschillende manieren splitsen in een product van twee veeltermen A(x) en B(x). Een van de mogelijkheden is:
A(x)=x(x+1)(x^2+x+1)(x^2-x+1)^2
=x^8+x^6+x^5+x^4+x^3+x
en
B(x)=x(x+1)(x^2+x+1)
=x^4+2x^3+2x^2+x.
De coëfficiënten en de machten van de veeltermen A(x) en B(x) laten zien dat deze ontbinding de twee dobbelstenen van Sicherman oplevert.
Een tweede opsplitsing is de triviale opsplitsing met A(x)=B(x), die opnieuw de twee gewone dobbelstenen oplevert.
A(x)=x(x+1)(x^2+x+1)(x^2-x+1)
=x^6+x^5+x^4+x^3+x^2+x^1
en
B(x)=x(x+1)(x^2+x+1)(x^2-x+1)
=x^6+x^5+x^4+x^3+x^2+x^1.
Een derde mogelijkheid voor de opsplitsing in een product van twee veeltermen is de volgende:
A(x)=(x+1)^2(x^2+x+1)(x^2-x+1)
=x^6+2x^5+2x^4+2x^3+2x^2+2x+1
en
B(x)=x^2(x^2+x+1)(x^2-x+1)
=x^6+x^4+x^2.
Nemen we eerst de dobbelsteen die overeenkomt met A(x) onder de loep. Deze dobbelsteen heeft de vorm van een dodecaëder waarop 1 keer de 6 voorkomt, 2 keer de 5, 2 keer de 4, 2 keer de 3, 2 keer de 2, 2 keer de 1 en 1 keer de 0. Dat het om een twaalfvlak gaat, is meteen duidelijk omdat de som van de coëfficiënten gelijk is aan 12.
Lege zijvlakken zijn eerder ongewoon bij dobbelstenen. Maar hier kan het niet anders. De veelterm A(x) eindigt op 1 \cdot x^0. Er moet dus 1 zijvlak met het cijfer 0 zijn.
De tweede dobbelsteen zou 1 keer de mogelijkheid moeten hebben om een 6 te gooien, 1 keer de 4 en 1 keer de 2. Dat zou bijvoorbeeld kunnen door de dobbelsteen te vervangen door een lange driehoekig prisma waarmee gerold wordt en waarop de cijfers 2, 4 en 6 staan. Hetzelfde effect krijgen we als we een kubus gebruiken en elk van de cijfers op twee zijvlakken zetten. Hierdoor wijzigen de kansen op 2, 4 en 6 niet.
Het alternatief voor de dobbelstenen van Sicherman dat we hier vonden, zie je op de ontvouwing van Figuur 4.
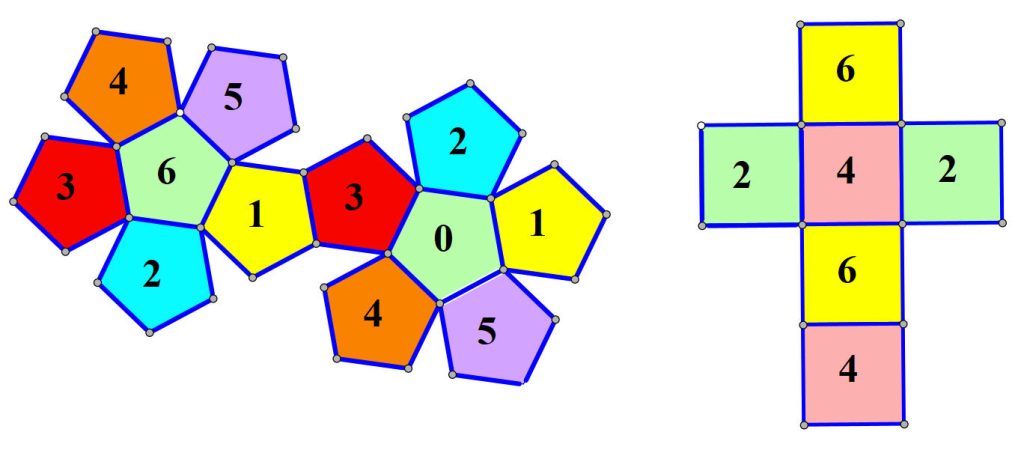
Figuur 4 – Een alternatief voor de dobbelstenen van Sicherman
Wil je het nog gekker maken dan dit dobbelstenenpaar, dan vind je vast nog andere mogelijkheden. UW-redactielid Alexander schreef een pythonprogramma om alle alternatieven te kunnen overlopen. Sommige opsplitsingen gaven veeltermen met negatieve coëfficiënten. Die moesten verworpen worden want het aantal keer dat een ogenaantal voorkomt, is een natuurlijk getal. Alexander vond buiten de mogelijkheden die reeds aan bod kwamen enkel nog mogelijkheden met dobbelstenen met 9 zijvlakjes en met 18 zijvlakjes. Die leken ook niet meteen geschikt voor gebruik. Er zijn immers geen eenvoudige regelmatige ruimtelichamen bekend met 9 of met 18 zijvlakjes. Op de webshop van Dungeons and Dragons, de toonaangevende dobbelstenenproducent, zijn deze dobbelstenen niet verkrijgbaar. Een noodoplossing voor een dobbelsteen met 9 vlakjes zou een lichaam zijn met twee regelmatige negenzijdige piramiden die met de basissen aan elkaar gekleefd zijn.
Kan het ook met drie dobbelstenen?
Ja, dat lukt. Kijk maar eens naar de volgende veeltermen A(x), B(x) en C(x) waarvan het product precies gelijk is aan de hierboven vermelde veelterm x^2(x+1)^2(x^2+x+1)^2(x^2-x+1)^2.
A(x)=(x+1)^2(x^2-x+1)^2
=x^6+2x^3+1
en
B(x)=C(x)=x(x^2+x+1)
=x^3+x^2+x.
De interpretatie van deze veeltermen is duidelijk. A(x) staat voor een dobbelsteen in de vorm van een regelmatig viervlak. De cijfers op de zijvlakken zijn 6, 3, 3 en 0. De veeltermen B(x) en C(x) staan voor een kubusvormige dobbelsteen met op twee zijvlakken een 3, twee zijvlakken een 2 en op de laatste twee zijvlakken een 1. Dat er twee gelijke dobbelstenen gebruikt worden, maakt dit alternatief voor Sicherman een beetje saai, als je het mij vraagt.
Kan het ook met negatieve getallen?
Ook dit lukt. Als je cijfers met een toestandsteken op een zijvlak van een dobbelsteen wil vermijden, kun je met groene stippen werken voor een positief aantal ogen en met rode stippen voor een negatief aantal ogen.
Er is een eenvoudige manier om de twee saaie dobbelstenen met de getallen 1, 1, 2, 2, 3 en 3 te vervangen door ongelijke dobbelstenen. Verminder de ogenaantallen van de eerste dobbelsteen bijvoorbeeld met 2 en verhoog de ogenaantallen van de andere dobbelsteen met 2. Bij een dobbelworp met de twee dobbelstenen zullen de +2 en de -2 elkaar in de som altijd compenseren. Voor de kansverdeling van de som maakt deze aanpassing dus helemaal niets uit.
We kunnen dit ook algebraïsch verklaren. Vermenigvuldig de veelterm B(x) met x waardoor de exponenten (en dus ook de aantallen ogen) met eentje verhogen. Deel de veelterm C(x) door x. Hierdoor worden alle exponenten met eentje verlaagd. Als je het product van de twee nieuwe veeltermen neemt, compenseert de vermenigvuldiging met x de deling door x. De kansverdeling blijft hiermee behouden.
In Figuur 5 zie je de ontvouwing van de nieuwe dobbelstenen: een tetraëder met de getallen 0, 3, 3 en 6, een kubus met de getallen -1, 0 en 1 (telkens twee keer) en een kubus met de getallen 3, 4 en 5 (telkens twee keer). Dit leuke trio doet hetzelfde als een gewoon dobbelstenenpaar.
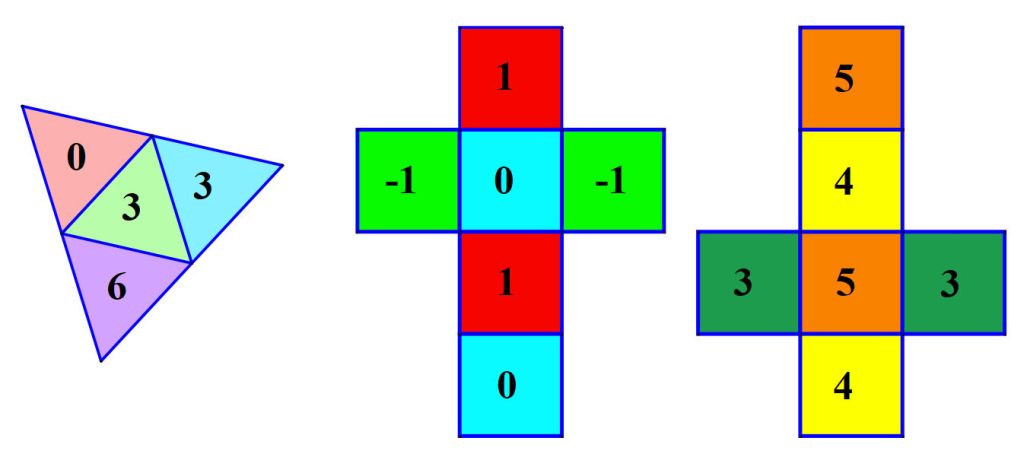
Figuur 5 – Een nieuw alternatief voor de dobbelstenen van Sicherman
Onderzoeksvraag voor leerlingen
Het is een goede onderzoeksvraag voor leerlingen om de kansverdeling van deze drie dobbelstenen op te stellen vanuit hun intuïtie. Een mogelijkheid om dit te doen, is door eerst te kijken naar een worp met de twee kubusvormige dobbelstenen.
De mogelijkheden voor de som T zie je in Figuur 6. In dit diagram zie je weer de vertrouwde diagonalen. Daarna beschouw je de som van de worp T (met twee kubusvormige dobbelstenen) en de worp met de tetraëderdobbelsteen. Deze sommen van drie dobbelstenen noemen we D.
Een overzicht van de som D van de drie dobbelstenen vind je in ook in Figuur driegekkestenen}. In de verticale rand som je de vier ogenaantallen van de tetraëder (0, 3, 3 en 6) op. In de horizontale rand noteer je de ogenaantallen van de worp met de twee kubussen (2, 3, 3, 4, 4, 4, 5, 5, 6). Als je goed naar de kleuren in de tabel kijkt, kom je tot dezelfde kansverdeling als bij de normale dobbelstenen N aan het begin van dit artikel.
Ziezo, het speurwerk zit er ongeveer op. Voor het ontwerpen van dobbelstenen met rationale getallen op de zijvlakken, heb ik geen spannende dingen meer ontdekt.
Mocht jij, beste lezer, me een van deze dobbelstenenparen kunnen 3D-printen of mocht je me een code voor een 3D-printer kunnen bezorgen, het zou me erg plezieren. En het zou me volgend schooljaar heel wat knip- en plakwerk besparen.
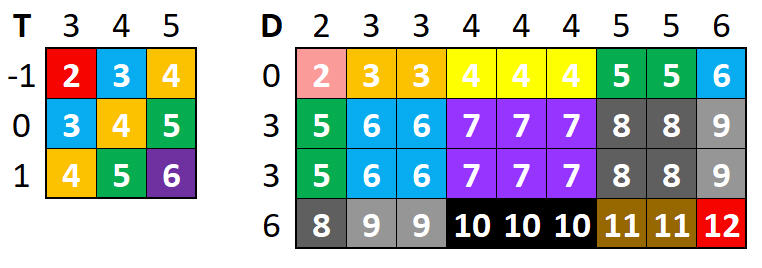
Figuur 6 – Alle mogelijke worpen met de twee kubusvormige dobbelstenen (T) en met de drie dobbelstenen (D)
Wetenschappelijk onderzoek
In 1978 na de ontdekking van de Sichermandobbelstenen werd in verschillende wetenschappelijke kringen de vraag gesteld naar andere gekke dobbelstenen. De wereldberoemde puzzeluitdenker Martin Gardner opperde in de Scientific American dat er slechts één alternatief was voor twee gewone kubusvormige dobbelstenen met twee ongewone kubusvormige dobbelstenen. Maar hij had wellicht nog niet nagedacht over een uitbreiding naar het probleem met $n$ dobbelstenen met elke $m$ zijvlakken.
Hierover publiceerden Joseph A. Gallian en David J. Rusin in 1979 een paper, zie bronnen. Ze onderzochten zelf geen oplossingen waarbij er dobbelstenen met een ongelijke vorm gecombineerd werden. In de laatste paragraaf van hun publicatie vermeldden ze wel de 18-zijdige dobbelsteen die gecombineerd kon worden met de tetraëder. Die vonden wij dan weer minder geschikt voor klasgebruik.
Bronnen
- Sicherman Dice. Wikipedia \url{https://en.wikipedia.org/wiki/Sicherman_dice}.
- Gallian, J. A., Rusin D. J. (1979). Cyclotomic polynomials and nonstandard dice. Discrete Mathematics 27, p.245-259. North-Holland Publishing Company.






 Onder de loep
Onder de loep