Labyrinten en doolhoven

Wim Kleijne

Epsilon Uitgaven in samenwerking met de Nederlandse Vereniging van Wiskundeleraren

Amsterdam, 2015, ISBN 978 90 5041 148 6

Uit de Zebra-reeks

In de Nederlandse Zebra-reeks zijn er ondertussen al meer dan 70 boekjes verschenen, die leerlingen uit de laatste jaren van het middelbaar onderwijs kunnen aanzetten om zelf een interessant wiskundig onderzoek te doen naar een onderwerp dat soms op het eerste gezicht weinig verband houdt met wiskunde. Het laatst uitgegeven boekje gaat over origami. Het voorlaatste over minimale art objecten. En het derdelaatste over de wiskunde van de Dambusters, bommenwerpers uit de tweede wereldoorlog die Duitse dammen met precisie onder vuur moesten nemen.

Misschien hebben we het over deze onderwerpen later nog eens. Nu zou ik een woordje willen vertellen over <em>Labyrinten en doorhoven}, Zebra-boekje 44, geschreven door Wim Kleijne, Nederlandse wiskundige en filosoof, voormalig onderwijsinspecteur en voorzitter van de staatsexamens. Het boekje blinkt uit door de mooie culturele illustraties die beginnen in de tijd van de mythologische Minotaurus die opgesloten was in het labyrint van Knossos en eindigen bij de moderne doolhof uit 1978 in de tuin van het kasteel van Leeds in Kent. Het werk wekt interesse door de wiskunde die erin uitgeschreven staat, maar vooral ook door de wiskunde die er niet in uitgeschreven staat. Zelf werd ik meteen aangezet om opzoekingen te doen. Ik denk dat leerlingen dezelfde drang voelen wanneer ze het Zebra-boekje doornemen.

Figuur 1 Voorpagina van Labyrinten en doolhoven

Wiskundige karakteristieken van een labyrint

Meestal gebruiken we de termen labyrint en doolhof door elkaar, alsof het synoniemen zouden zijn. Er is echter een groot verschil. Bij een labyrint hoef je niet te zoeken hoe je moet lopen om je doel te bereiken. Het heeft geen kruispunten, geen doodlopende wegen, geen eilanden waar je eindeloos rond kunt cirkelen. Om een labyrint te doorlopen hoef je niet slim te zijn. Je volgt de weg die nu eens linksom draait en dan weer rechtsom. Bij een doolhof komen bovenstaande moeilijkheden wel voor. Je moet echt wel handigheid aan de dag leggen om in het midden te raken of om bij de uitgang te komen. Dit Zebra-boekje zoomt voornamelijk in op labyrinten.

De eerste vraag die opgelost wordt, is: ‘Wanneer kunnen we twee labyrinten wiskundig als verschillend beschouwen?’ Net zoals in de topologie beschouwen we de labyrinten als van rubber. Je kunt ze zo vervormen dat je telkens wanneer je van omloopzin verandert, je op een andere diepte zit. Je kunt de vorm van de wegen ook soepel kneden tot ze min of meer cirkelvormig zijn. En je kunt er ook voor zorgen dat de overgangen van de ene naar de andere diepte allemaal op dezelfde straal van de cirkel liggen. Verderop zie je hier twee voorbeelden van.

Aanvankelijk was ik in de waan dat je alleen moet weten hoeveel keer je van omloopzin moet veranderen bij het doorlopen van het labyrint om de structuur van het labyrint vast te leggen. Maar al spoedig bleek dat dit niet voldoende is.

In Figuur 2 zie je twee labyrinten met een diepte van 8 niveaus. Die niveaus kun je aflezen door een lijnstuk te tekenen van buiten het labyrint naar het centrum dat zoveel mogelijk muren van het labyrint snijdt. Op dit lijnstuk geef je de dieptes aan. Het buitengebied heeft diepte 0 en het centrum heeft diepte 8. Als je deze twee labyrinten van buiten naar binnen doorloopt, begin je bij niveau 0 en ga je dan naar niveau 3. Tot hier toe zijn ze identiek. Maar verderop verschillen ze. Je kunt nagaan dat het linkse labyrint niveaurij 0-3-2-1-4-7-6-5-8 heeft, het rechtse labyrint heeft niveaurij 0-3-6-5-4-7-2-1-8. De niveaurijen zijn verschillend. Bijgevolg zijn de twee labyrinten topologisch verschillend.

Niveaurijen zijn essentieel bij het bestuderen van labyrinten. Elk labyrint heeft een uniek bepaalde niveaurij. Maar of elke niveaurij met een deugdelijk labyrint overeenkomt, moeten we nog onderzoeken.

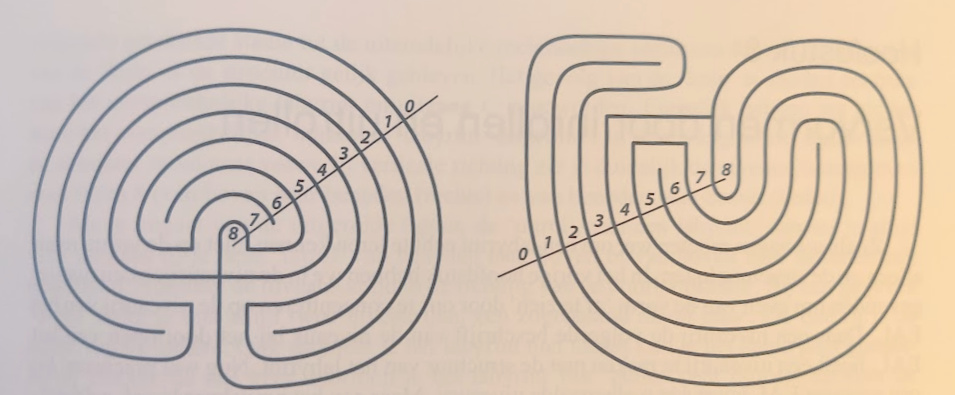
Figuur 2 Twee verschillende labyrinten met diepte 8

Niveaurijen van een EAL

Een deugdelijk labyrint wordt gedefinieerd als een EAL, een Enkelvoudig Alternerend Labyrint. We verklaren hieronder de drie letters en geven zonder bewijs aan hoe je deze kenmerken om kunt zetten in voorwaarden voor de bijbehorende niveaurij.

Een labyrint is enkelvoudig (E) als het niet uiteenvalt in meerdere kleine labyrinten. Dit probleem zou je bijvoorbeeld kunnen hebben als je slingerend van het buitengebied naar het centrum loopt, van daaruit een rechtstreekse doorsteek naar het buitengebied neemt en dan weer slingerend naar het centrum gaat. Bij een enkelvoudig labyrint begint de niveaurij met 0, eindigt ze met de diepte (hier 8) en komen alle andere niveaus tussenin precies één keer aan bod. Dit is de gemakkelijkst te begrijpen voorwaarde van de drie.

Een labyrint is alternerend (A) als er bij elke verwisseling van niveau ook van omloopzin gewisseld wordt. Het is al heel wat moeilijker te bewijzen dat deze voorwaarde overeenkomt met het afwisselen van even en oneven getallen in de niveaurij.

De belangrijkste voorwaarde voor een labyrint (L) is dat de wegen niet kruisen. Hoe we dit kunnen afleiden uit de niveaurij leggen we uit aan de hand van het linkse labyrint met niveaurij 0-3-2-1-4-7-6-5-8. Neem alle koppels van opeenvolgende getallen die beginnen met een even getal: \((0,3)\), \((2,1)\), \((4,7)\) en \((6,5)\). Als we deze koppels omzetten in lijnstukken (\([0,3]\), \([1,2]\), \([4,7]\) en \([5,6]\)) dan zien we dat sommige lijnstukken andere omvatten. De lijnstukken zullen elkaar nooit gedeeltelijk overlappen. Deze eis geldt niet alleen voor de <em>even koppels} in de niveaurij van een labyrint (d.w.z. de koppels die beginnen met een even getal). Ze geldt ook voor de oneven koppels}.

Ziezo, vanaf nu is het technisch mogelijk om uit te zoeken hoeveel verschillende labyrinten er bestaan met diepte acht zonder nog aan labyrinten te denken. Een computer kan alle niveaurijen onderzoeken en nagaan of ze aan de drie eisen (E, A en L) voldoen. Wil je het antwoord nu al weten voor labyrinten met diepte 8? Het zijn er 42. Twee ervan ken je al.

Misschien een teleurstellende opmerking (of net een uitdagende): er is op dit ogenblik nog altijd geen formule gevonden om te berekenen hoeveel verschillende AEL’s er bestaan van niveau \(n\). Wel weten we dat het aantal AEL’s exponentieel stijgt in functie van \(n\). Dat wordt mooi aangetoond in het Zebra-boekje.

Uitgerolde labyrinten en opgevouwen stroken postzegels

Om nog een beter zicht te krijgen op de structuur van EAL’s, knippen we het ronde labyrint open langs de straal \([AB]\) tussen de plaatsen waar de baan van omloopzin wisselt.

Daarna vervormen we het ronde labyrint stapsgewijze tot een rechthoek. Deze rechthoekige vorm maakt het veel eenvoudiger om grip te krijgen op en om bewijzen te leveren over labyrinten. In Figuur 3 zien we dat de ingang van het labyrint bovenaan rechts ligt en de uitgang onderaan links. Alle wisselingen van niveaus zitten nu aan de buitenkant van het rechthoekige labyrint.

Dit rechthoekige diagram heeft wel iets weg van het zijaanzicht van een drie keer dubbelgevouwen hoeslaken in mijn slaapkamerkast. Dit is meteen ook de link naar de volgende stap in de redenering. We maken een omweggetje naar het vouwen van een papierstrook en koppelen dit aan de Catalangetallen, vernoemd naar de in Brugge geboren wiskundige Eugène Charles Catalan (1814-1894).

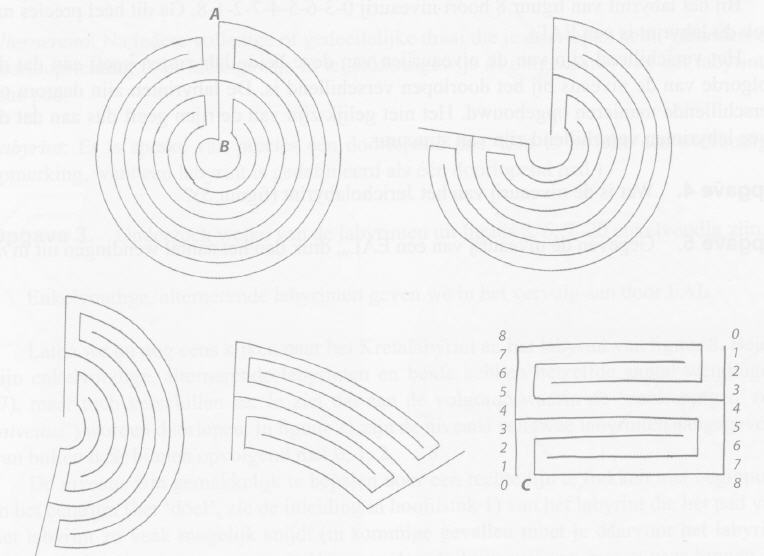
Figuur 3 Openknippen van een rond labyrint

Beeld je een strook van vijf postzegels in die met geperforeerde vouwlijnen aan elkaar hangen. Je kunt de postzegels zigzag samenvouwen tot een stapeltje. Dat is de meest gebruikelijke manier op ze op te vouwen. Mochten de perforatielijnen rekbare stroken zijn dan bestaan er nog heel wat andere manieren om de postzegels samen te vouwen. In Figuur 4 zie je dat er 14 verschillende manieren zijn (gesteld dat alle postzegels er identiek uitzien). Over postzegelstroken is al heel wat onderzoek gedaan. Het aantal manieren om \(n\) identieke postzegels samen te vouwen wordt gegeven door het \(n\)-de Catalangetal \(C_n\) waarbij

\(C_n=\frac{(2n)!}{(n+1)!\cdot n!}.\)

Deze formule bevestigt dat er 14 stapeltjes van 5 postzegels mogelijk zijn. Reken maar na.

Als je wat langer kijkt naar deze schema’s dan wordt de verwantschap met de uitgerolde labyrinten duidelijk. In elk stapeltje stelt de bovenste postzegel niveau 0 voor, de tweede postzegel niveau 1 … en de vijfde postzegel niveau 4. We zoeken dus naar stapeltjes die labyrinten met diepte 4 kunnen voorstellen. Net zoals bij de uitgerolde labyrinten, zitten ook hier de veranderingen van omloopzin aan de buitenkanten.

Echter, de 14 schema’s komen niet allemaal in aanmerking om een uitgerold labyrint voor te stellen. Om bovenaan naar binnen te kunnen gaan en onderaan naar buiten, moeten de losse eindjes van de stapel bovenaan en onderaan zitten. Er zijn bijgevolg slechts twee van deze schema’s geschikt om een labyrint voor te stellen: het eerste van de bovenste rij en het laatste van de bovenste rij.

Het eerste schema van de bovenste rij stelt de triviale zigzagstapeling van postzegels voor. Het bijbehorende labyrint bestaat enkel uit zigzagwandelingen naar de volgende diepte. De niveaurij is 0-1-2-3-4. Wiskundigen vinden dit triviale labyrint weinig interessant.

Het laatste schema van de bovenste rij is minder triviaal. Het bijbehorende labyrint heeft niveaurij 0-3-2-1-4. Hiermee is aangetoond dat er slechts één niet triviaal labyrint met diepte 4 bestaat.

Via de methode van het postzegelvouwen kunnen computers beperkt verder gaan om uit te zoeken hoeveel niet triviale labyrinten er bestaan van andere diepten. In dit Zebraboekje worden de resultaten getoond tot en met diepte 22. Een indrukwekkende prestatie.

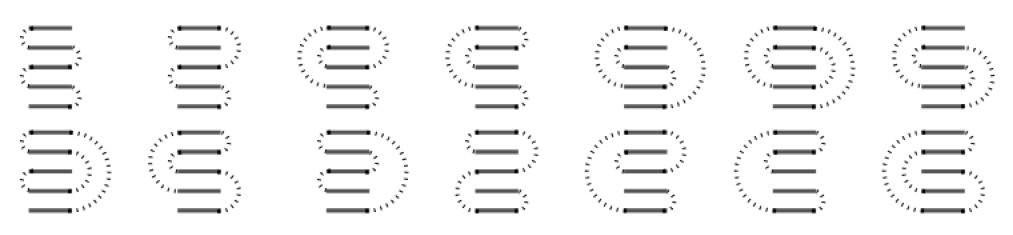
Figuur 4 Een strook van 5 postzegels kan op 14 manieren opgevouwen worden

Ik eindig deze bespreking graag met een kleine opdracht voor de lezer. Zet het laatste schema van de bovenste rij om in een uitgerold rechthoekig labyrint en vervorm dit daarna stapsgewijze tot een cirkelvormig labyrint. Voilà, je hebt nu het enige niet triviale labyrint met diepte 4 uitgetekend. Perfect voor een haagconstructie in je achtertuin.

BRONNEN

Dickau, R. Unlabeled Stap Folding. https://www.robertdickau.com/unlabeledfoldings.html