Zeven jaar geleden besprak ik al een kunstwerk van de jaarlijkse Artefact-tentoonstelling in Stuk te Leuven (Roelens, 2017). Toen ging het over het werk Squaring the Circle van het kunstenaars-collectief Troika: een metalen ruimtekromme die je vanuit de ene kant ziet als een cirkel en vanuit de andere kant als een vierkant. Ook op de laatste editie, in februari 2024, stond een kunstwerk dat mij wiskundig inspireerde: Untitled Circle Brass (Koperen cirkel zonder titel).
Het kunstwerk
Op de grond ligt een ellipsvormige koperen spiegel. Een lamp, op de juiste plaats opgehangen, zorgt ervoor dat er op de muur een lichtvlek ontstaat met de vorm van een perfecte cirkel.
Volgens de uitleg in de brochure had de Nederlandse kunstenares Germaine Kruip per toeval een cirkelvormige lichtvlek op de muur van haar studio waargenomen en is zij op zoek gegaan naar hoe ze dit fenomeen opnieuw kon creëren.
Ik neem me voor om dit kunstwerk eens aan mijn leerlingen te beschrijven en er een foto van te tonen, in eerste instantie zonder duidelijke vragen of opdrachten. In gesprek met hen kunnen er eventueel preciezere vragen over de wiskunde achter dit werk opduiken.
Eerst wil ik zelf proberen te begrijpen welke wiskunde achter dit werk zit.

Figuur 1 Foto die ik op de tentoonstelling maakte
Verklaring voor de cirkelvormige lichtvlek
Het is niet eenvoudig om de ellipsvormige spiegel en de lamp zo te plaatsen dat de lichtvlek een perfecte cirkel vormt. Ik stel voor om het om te keren: vertrekkend van de lamp en de cirkel op de muur, bepalen welke ellips op de grond nodig is. Zo zou de kunstenares het gedaan kunnen hebben. Na deze berekeningen zou ze dan de juiste spiegel kunnen maken of bestellen.
Nog eenvoudiger wordt het als ik de cirkel in gedachten ten opzichte van de vloer spiegel. Het spiegelbeeld is een even grote cirkel onder de grond, op het verlengde van de muur of op de muur een verdieping lager (zie Figuur 2). Dan is de gezochte ellips de doorsnede met de vloer van de schuine kegel met als grondvlak de gespiegelde cirkel en als top de lamp. Vanaf hier hoef ik niet meer te denken aan een spiegel en een lichtvlek, maar gaat het over een schuine cirkelkegel die gesneden wordt met een vlak (de vloer).
Apollonios van Perga bestudeerde in de derde eeuw v.C. schuine cirkelkegels (schuine kegels met cirkelvormige grondvlakken). Hij toonde aan dat de doorsnede van een schuine cirkelkegel met een vlak, wanneer die doorsnede begrensd is, inderdaad een ellips vormt. Ook het omgekeerde geldt: de kegel bepaald door zo’n ellipsvormige doorsnede en de top, bevat cirkelvormige doorsneden.
Bovendien toont Apollonios aan dat er in een schuine cirkelkegel twee vlakkenrichtingen zijn van cirkelvormige doorsneden. Dat is stelling I,5 in zijn werk Konika (zie bv. de Graaf en Roelens, 2013, p. 28). Bij de opstelling van Germaine Kuip is de vlakkenrichting van de muur één van deze twee, maar de stelling van Apollonios zegt dat er nog een andere vlakkenrichting van cirkelvormige doorsneden bestaat. Ik wou niet opvallen in de tentoonstelling, maar anders was ik teruggekomen met een groot vlak stuk karton om in de weerkaatste lichtbundel andere cirkelvormige lichtvlekken te vangen, niet evenwijdig met de muur…
De assen van de ellipsvormige spiegel
Op Figuur 2 zie je een zijaanzicht van de situatie. L is de lamp, [AB] de gespiegelde cirkel onder de vloer en [A’ B’] de ellips op de vloer. L’ is de loodrechte projectie van L op de muur.
Ik wil de assen van de ellips bepalen in functie van:
- de hoogte h van de lamp;
- de afstand d van de lamp tot de muur;
- de hoogte m van het middelpunt van de cirkel;
- de straal r van de cirkel.
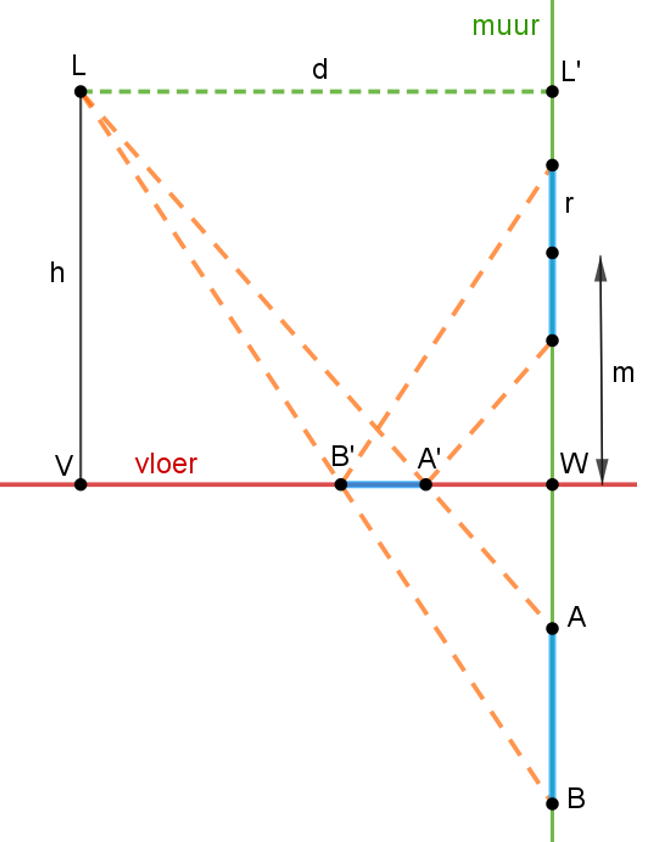
Figuur 2 De situatie in zijaanzicht
De kleine as bepalen in een zijaanzicht
De kleine as van de ellips is |A’ B’|. Die kan ik berekenen met gelijkvormige driehoeken in Figuur 2.
Omdat \Delta B’LV \sim \Delta LBL’ en \Delta A’LV \sim \Delta LAL’, hebben we:
|A’B’| = |VA’|-|VB’|
= \frac{d\cdot h}{|L’A|}-\frac{d\cdot h}{|L’B|}
= d h \left(\frac{1}{h+m-r}- \frac{1}{h+m+r} \right)
=\frac{2dhr}{(h+m)^2-r^2}.
De grote as bepalen in een vooraanzicht
De kleine as kon met vlakke meetkunde in het zijaanzicht worden berekend. Dit komt omdat de kleine as de projectie vanuit L op de vloer is van de verticale middellijn [AB] van de (ondergrondse) cirkel. Mijn eerste idee was dat de grote as van de ellips op analoge wijze de projectie vanuit L op de vloer zou zijn van de horizontale middellijn van de cirkel. Maar Figuur 3 maakt meteen duidelijk dat dit niet zo is!
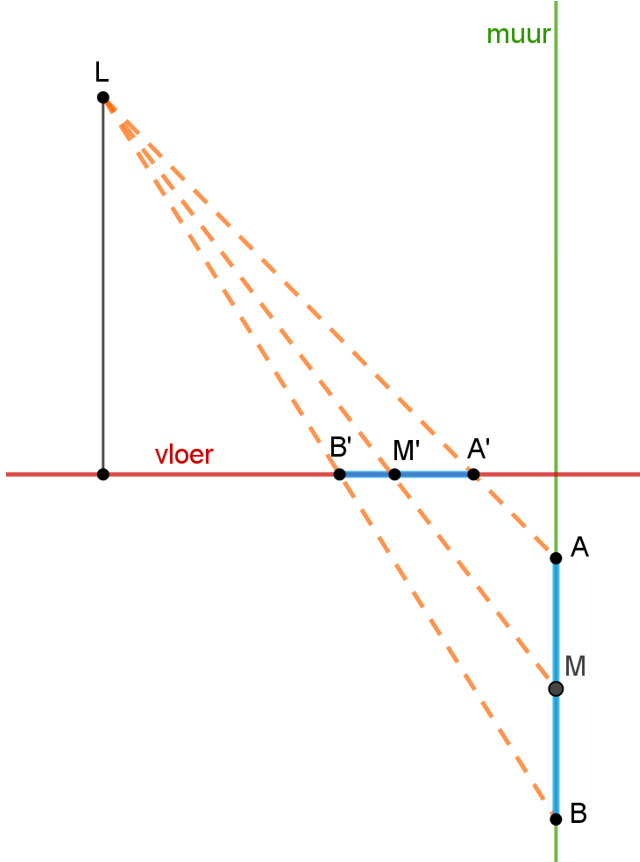
Figuur 3 M’ is niet het midden van [A’B’]
De middellijn van de cirkel door M en loodrecht op deze tekening komt overeen met de koorde in de ellips door M’ en loodrecht op deze tekening. Maar M’ is niet het middelpunt van de ellips. De stelling van Thales geldt immers enkel voor evenwijdige projectie, niet voor projectie vanuit een punt (hier L).
Hoe kunnen we de grote as van de ellips bepalen in functie van dezelfde afmetingen als we deden voor de kleine as?
Eén manier is een assenstelsel invoeren in de ruimte, een parameter- of cartesiaanse vergelijking van de kegel bepalen en een vergelijking voor de vlakke doorsnede met de vloer zoeken. Ik heb dat gedaan en het is mij gelukt, maar het lijkt me weinig zinvol deze zware berekeningen hier op te nemen.
Een ander idee is nagaan welke koorde van het cirkelvormig grondvlak van de kegel overeenkomt met de grote as van de ellipsvormige doorsnede.
Een 3D-figuur in GeoGebra gaf mij de oplossing.
De grote as van de ellips is zo dat de raaklijnen in de eindpunten loodrecht staan op de muur. Dit zijn de raaklijnen PP’ en QQ’ in Figuur 4. Om ook de kegel zichtbaar te maken, heb ik gewerkt met een spoor.
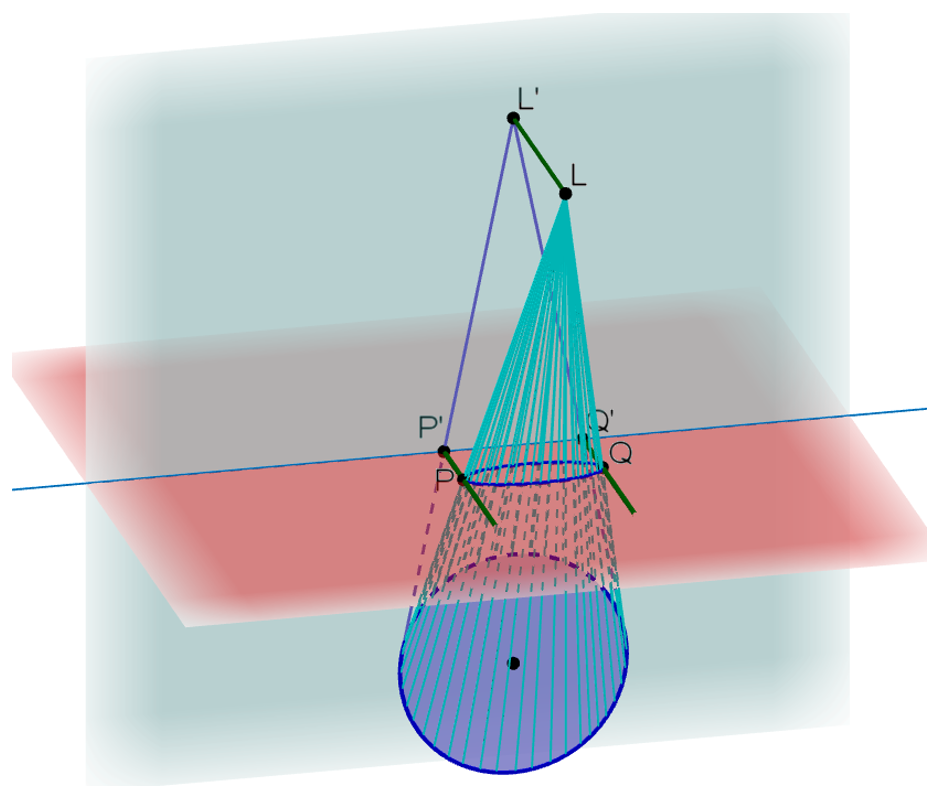
Figuur 4 3D-figuur in GeoGebra
Samen met de lamp L, de top van de kegel, vormen deze raaklijnen twee vlakken loodrecht op de muur, die elkaar snijden in LL’ (zie Figuur 5). Deze vlakken raken aan de kegel en dus ook aan het cirkelvormige grondvlak. De raakpunten R en S bepalen de koorde die door de centrale projectie vanuit L op de vloer afgebeeld wordt op de grote as [PQ] van de ellips (zie Figuur 5).
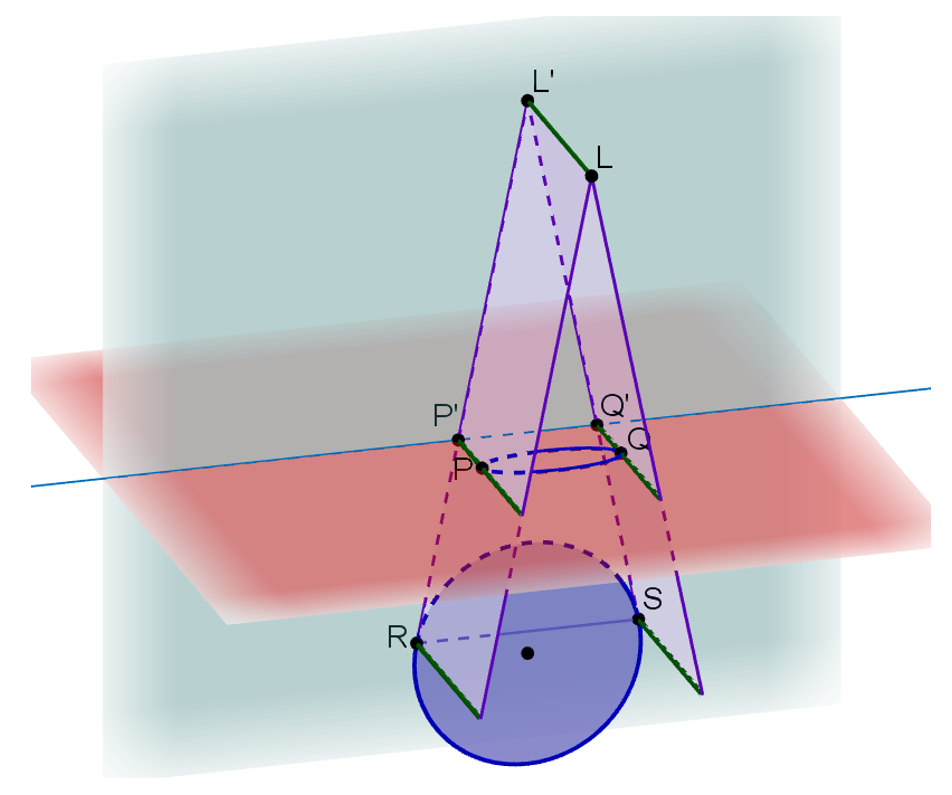
Figuur 5 De twee raakvlakken
Opnieuw kunnen we alles oplossen met vlakke meetkunde: het verband tussen de grote as van de ellips en de gegevens wordt helemaal bepaald door het loodrechte aanzicht op de muur (zie Figuur 4).
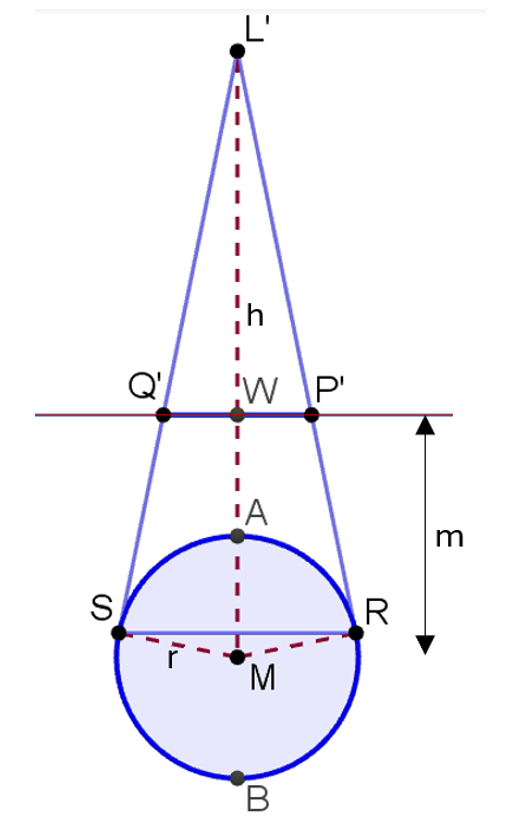
Figuur 6 De vlakke situatie op de muur
Ik herinner me van de lessen analytische meetkunde die ik in de jaren tachtig gaf, dat de rechte RS de poollijn van punt L’ ten opzichte van de cirkel genoemd wordt. Maar we hebben hier geen theorie over poollijnen nodig.
Laten we de lengte |PQ| van de grote as bepalen ten opzichte van de gegevens. We steunen op de gelijkvormigheid van de driehoeken L’P’W en L’MR (hoek-hoek: ze hebben hoek \hat{L’} gemeenschappelijk en ze hebben allebei een rechte hoek).
|PQ| = |P’Q’|
= 2|P’W|
= 2\frac{r\cdot h}{|L’R|}
= \frac{2rh}{\sqrt{(h+m)^2-r^2}}
De formule voor de grote as heeft opvallende gelijkenissen met die voor de kleine as. Op de wortel na staat hetzelfde in de noemer, en nu staat er geen factor d in de teller. Dit laatste begrijp ik: de afstand van de lamp tot de muur beïnvloedt het ‘vooraanzicht’ niet…
Concrete getallen invullen
Laten we concrete getallen invullen en zien of we geloofwaardige resultaten uitkomen.
Neem aan dat de lamp 4 meter boven de grond hangt (h=4) en op 2,5 meter van de muur (d=2,5). Neem 2 meter voor de hoogte van het middelpunt en 1 meter voor de straal van de cirkelvormige lichtvlek (m=2, r=1). Dan krijgen we voor de kleine as van de ellips:
\frac{2dhr}{(h+m)^2-r^2}\approx 0,57
en voor de grote as:
\frac{2rh}{\sqrt{(h+m)^2-r^2}} \approx 1,35.
Wel ja, dit zou kunnen…
Achteraf zie ik dat het boekje van de tentoonstelling de afmetingen van de spiegel vermeldt: 1,22 meter bij 0,35 meter. Ook de diameter van de cirkelvormige lichtvlek staat erbij: 1,60 meter (dus r=0,80). De hoogte van de lichtvlek en de positie van de lamp staan er niet bij. Door wat te proberen met een rekenblad, kan ik de juiste afmetingen voor de assen van de ellips verkrijgen met: h=4,5; d=1,75; m=1,5; r=0,8. Dit zal wellicht niet de enige mogelijkheid zijn, maar op die manier zou het mij dus lukken om het kunstwerk na te maken …
BRONNEN
- de Graaf, W., Roelens, M. (2013). Het astrolabium. Uitwiskeling 29/4.
- Roelens, M. (2017). Een vierkante cirkel. Uitwiskeling 33/3.


