Rik Verhulst, Wiskunde voor bollebozen

Gompel en Svacina, Oud-Turnhout, 2018,
ISBN 9789463710657

De bollebozen uit de titel zijn leerlingen van de laatste jaren van de basisschool of de eerste (of tweede) graad van het secundair onderwijs. Er is weinig wiskundige voorkennis nodig en alles wordt geleidelijk opgebouwd en helder uitgelegd. Ik denk niet dat je hoogbegaafd moet zijn om tot het bollebozen-leespubliek te behoren. Wel moet je nieuwsgierig zijn naar andere wiskundeonderwerpen dan in de klas en de tijd nemen om de opgaven te maken. Het boek doet een beetje handboekachtig aan, met oefeningenreeksen om de leerstof te verwerken. Anders dan in handboeken staan achteraan niet enkel de eindantwoorden maar uitgewerkte oplossingen, waardoor het boek geschikt is om zelfstandig door te nemen. Bij elk hoofdstuk is ook een appendix met historische of culturele achtergrond bij het onderwerp.

De figuren zijn verzorgd, met functioneel kleurgebruik. Ik vind het lettertype erg groot in verhouding tot de interlinie. Maar laten we vooral focussen op de inhoud.

Het boek bestaat eigenlijk uit twee delen. De eerste vijf hoofdstukken handelen over talstelsels, modulorekenen en codes. Hoofdstuk 6, ‘meetkunde van het ruitjespapier’ is plots iets helemaal anders en gaat over de zogenaamde ‘taxi-afstand’.

Bij wie ‘In de ban van de wiskunde’ gelezen heeft, zal de sobere stijl van dit boek meteen opvallen. In zijn vorige boek showde Verhulst een indrukwekkend panorama aan wiskundige onderwerpen, met veel culturele achtergrond maar ook vooral pittige wiskundige passages en onderwerpen die ik in mijn bespreking in Uitwiskeling 23/3 ‘typisch Verhulst’ heb genoemd: straffe verzamelingenleer met equivalentierelaties, partities en kardinaalgetallen, een oneindige stapel van torussen als model voor een exotische soort getallen, recursieve algoritmen en nomogrammen voor worteltrekking … In vergelijking hiermee is dit boek een toonbeeld van rust. Is Verhulst in die tussentijd dan toch een beetje gekalmeerd? Of is dit boek een illustratie van zijn veelzijdigheid aan stijlen en registers, aangepast aan het doelpubliek?
Hieronder vertel ik iets over de inhoud van het boek, zonder teveel te ‘spoilen’.

Talstelsels, modulorekenen en codering

Het principe van het vertrouwde tientallig stelsel wordt uitgebreid tot talstelsels met andere grondtallen dan \(10\). De lezer leert hiermee rekenen en cijferen. Dan volgt het klokrekenen (rekenen modulo \(12\)) en het modulorekenen met andere moduli dan \(12\), met veel oefeningen. In appendices verneemt de lezer iets over toepassingen van het modulorekenen: de controlecijfers in ISBN-nummers, kredietkaartnummers en streepjescodes. Ook Gauss komt ter sprake en het idee van een ‘groep’. Diezelfde Gauss stelde formules op waarmee je kunt bepalen voor welke waarden van \(N\) een regelmatige \(N\)-hoek wel of niet construeerbaar is met passer en liniaal.

De laatste twee hoofdstukken van dit eerste deel gaan over informaticatoepassingen van het binair talstelsel en het modulorekenen. Computers werken binair. Letters van het alfabet en andere tekens worden omgezet in getallen van zeven binaire cijfers (ASCII-codes). Berichten die je met een computer verstuurt, worden versleuteld zodat anderen dan de bestemmeling ze niet kunnen begrijpen. Dit gebeurt met modulorekenen en priemgetallen.

Meetkunde van het ruitjespapier

In een stad als New York moet een taxi de straten volgen, die een rechthoekig patroon vormen. De stad wordt vereenvoudigd tot ruitjespapier met vierkante ruitjes. De afstand tussen twee punten \(A\) en \(B\) op snijpunten van de lijntjes van het papier is de kortste afstand waarbij de lijnen gevolgd worden. Deze taxi-afstand \(\text{T}(A,B)\) is de som van het breedteverschil en het hoogteverschil van deze twee punten. Dit wordt dan veralgemeend tot punten die niet noodzakelijk op snijpunten van de lijntjes liggen. Als we in de meetkunde werken met deze taxi-afstand \(\text{T}\) in plaats van de euclidische afstand \(\text{E}\), ontstaan bizarre effecten. Zo is de driehoek \(ABC\) van figuur 1, die euclidisch een willekeurige driehoek is, volgens de taxi-afstand gelijkbenig, want \(\text{T}(A,B)=\text{T}(C,A)=4\). En de \(\text{E}\)-ruit \(KLMN\) is geen ruit meer voor de \(\text{T}\)-afstand.

Verhulst plaatst telkens mooi de euclidische meetkunde naast de taximeetkunde. Op die manier maakt hij van de gelegenheid gebruik om voor de lezers de euclidische meetkunde te herhalen of aan te vullen. Een loutere herhaling van schoolmeetkunde zouden zij wellicht minder boeiend vinden; hier hebben ze die herhaling nodig om de nieuwe wereld van de taxi-afstand te kunnen verkennen.

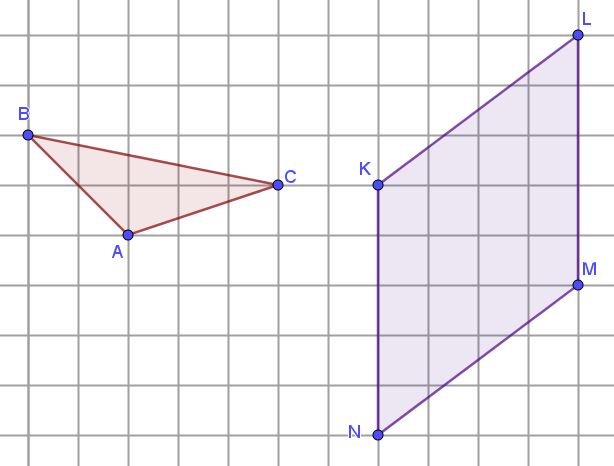
Figuur 1

Een \(\text{E}\)-cirkel met middelpunt \(M\) en straal \(r\) bestaat uit de punten op gelijke \(\text{E}\)-afstand tot \(M\). Vervang de \(\text{E}\)-afstand door de \(\text{T}\)-afstand en je hebt een \(\text{T}\)-cirkel. Maar zo’n \(\text{T}\)-cirkel ziet er euclidisch uit als een vierkant met diagonalen in de richting van de lijntjes van het ruitjespapier (figuur 2). De omtrek van een \(\text{E}\)-cirkel is \(4\) keer de diameter (in plaats van \(\pi\) keer bij de \(\text{E}\)-cirkel). Twee \(T\)-cirkels kunnen elkaar ‘innig raken’: oneindig veel punten gemeen hebben zonder samen te vallen (figuur 3).

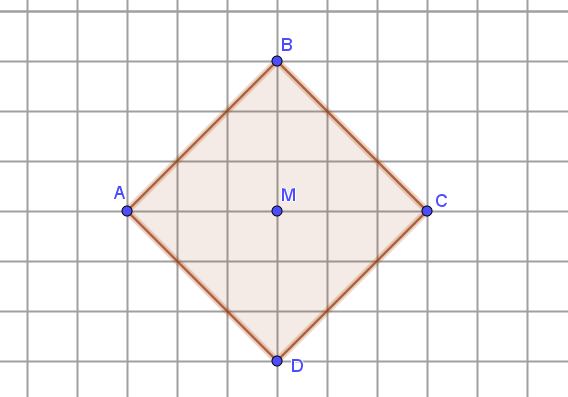
Figuur 2

Een mooie opgave is het bepalen van de \(\text{T}\)-middelloodlijn van een lijnstuk \([AB]\): de verzameling van de punten waarvan de \(\text{T}\)-afstanden tot \(A\) en tot \(B\) gelijk zijn. Je kunt die punten bepalen als snijpunten van \(\text{T}\)-cirkels met gelijke stralen en middelpunten \(A\) en \(B\). Behalve als \(A\) en \(B\) op een zelfde horizontale of verticale rechte liggen, is de \(\text{T}\)-middelloodlijn geen rechte meer! Er zijn zelfs gevallen waarbij de \(\text{T}\)-middelloodlijn geen gebroken lijn is maar volledige vlakdelen omvat… Vertrekkend van een eenvoudige definitie, die van de taxi-afstand, zijn de leerlingen in een bevreemdende wereld vol verrassingen terecht gekomen.

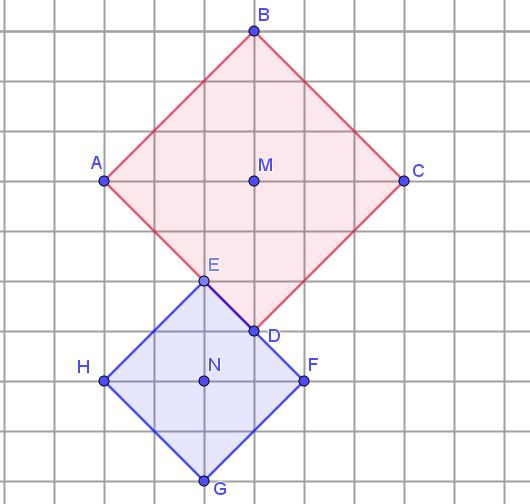
Figuur 3

Verhulst voert coördinaten en absolute waarde in en brengt de stelling van Pythagoras aan (de jonge lezers kennen dit immers nog niet). Hiermee kun je zowel de euclidische afstand als de taxi-afstand uitdrukken met formules. Voor twee punten \(P(x_1,y_1 )\) en \(Q(x_2,y_2 )\) geldt:

\(\begin{align}\notag
\text{T}(P,Q)&=|x_1-x_2|+|y_1-y_2|\\\notag
\text{E}(P,Q)&=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\
\end{align}\)

De volgende stelling wordt (met het nodige gevalsonderscheid) bewezen: als een driehoek \(\text{E}\)-gelijkzijdig is, dan is die niet \(\text{T}\)-gelijkzijdig. Hieruit volgt dan: als een driehoek \(\text{T}\)-gelijkzijdig is, dan is die niet \(\text{E}\)-gelijkzijdig. De jonge lezer maakt op die manier kennis met contrapositie.

Het boek sluit af met een beknopt overzicht van de geschiedenis van de meetkunde: Egypte, Thales, de school van Pythagoras, de Platonische lichamen, Euclides, Archimedes, niet-euclidische meetkunde.