Losanges 40 (2018), 13-20
De negenproef is door de beschikbaarheid van rekenmachines en computers (terecht) in onbruik geraakt. Dit artikel van Michel Ballieu (†2006), postuum gepubliceerd in Losanges, heeft niet als doel de negenproef in de lessen terug in te voeren. Maar los van het praktisch nut is het zowel wiskundig als historisch een boeiend onderwerp voor een beperkte onderzoeksopdracht.
Hoe werkt de negenproef?
Oudere collega’s kunnen dit stukje gerust overslaan. De negenproef dient om op een gemakkelijke manier rekenfouten te detecteren bij het ‘cijferen’. Het kan bij alle hoofdbewerkingen, maar we beperken ons hier tot een vermenigvuldiging. Bijvoorbeeld: 3587\cdot 286:
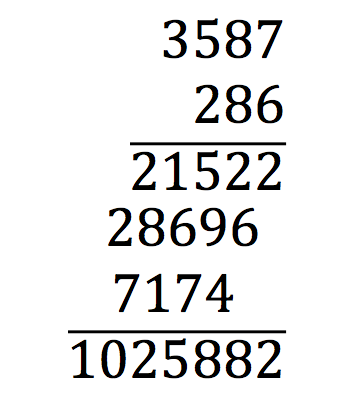
Je bepaalt de rest bij deling door 9 van beide factoren. In dit geval is dat 5 en 7. Die plaats je links en rechts in een X-vormig kruis. Je bepaalt de rest bij deling door 9 van het product 5\cdot 7=35. Dit is 8. Die plaats je bovenaan in het kruis. Dan bepaal je de rest bij deling door 9 van het product 1025882 dat je uitkomt. Dit is hier ook 8. Die plaats je onderaan in het kruis.
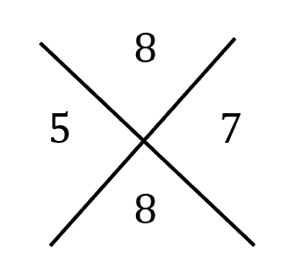
De getallen bovenaan en onderaan in het kruis moeten gelijk zijn, anders is er zeker een rekenfout gebeurd. Als die twee getallen gelijk zijn, is de kans groot dat je berekening juist is, maar waterdicht is de negenproef niet: je zou ook een fout gemaakt kunnen hebben die toevallig de rest bij deling door 9 onveranderd laat.
Waarom werkt de negenproef?
De rest van een natuurlijk getal a bij deling door 9 noteren we met a\mod 9 .
De negenproef voor de vermenigvuldiging van en steunt op de eigenschap
(a\cdot b) \mod 9 = \left((a\mod 9) \cdot (b \mod 9) \right) \mod 9
In woorden: de rest bij deling door 9 van het product is de rest bij deling door 9 van het product van de resten bij deling door 9 van de factoren. (Leuke volzin.) Om deze eigenschap te bewijzen, veronderstellen we dat de rest van a bij deling door 9 gelijk is aan r en dat de rest van b bij deling door 9 gelijk is aan s . Dan is a = 9u + r en b = 9v + S met u, v \in \mathbb{N}. Het product is
\begin{align*} a\cdot b &= (9u+r)(9v+s)\\ &= 9(9uv + us + vr) + r\cdot s.\end{align*}
De eerste term is een negenvoud en heeft dus geen invloed op de rest bij deling door 9. Hierdoor hebben a\cdot b en r\cdot s inderdaad dezelfde rest bij deling door 9.
Waarom juist 9?
De eigenschap waarop de negenproef steunt, geldt evengoed voor een ander getal dan 9. Ook de zevenproef en de elfproef zijn in de loop van de geschiedenis opgedoken. De zevenproef laat wel meer fouten onopgemerkt voorbij gaan. De mogelijke resten bij de zevenproef zijn 0,1,…, 6 en bij de negenproef 0,1,…,8. Hierdoor is de ‘kans’ bij de zevenproef groter om ‘toevallig’ dezelfde rest uit te komen.
Een groot voordeel van 9 is dat de rest bij deling door 9 heel gemakkelijk wordt bepaald: het is de som van de cijfers, of de som van de cijfers van de som van de cijfers, of… bv.
\begin{align*} 3587 \mod 9 &= 23 \mod 9\\ &= 5 \mod 9.\end{align*}
Immers:
\begin{align*} 3587 &= 3\cdot 1000 + 5\cdot 100 + 8 \cdot 10 + 7 \\ &=3(9\cdot 111 + 1) + 5(9\cdot 11 + 1) + 8(9\cdot 1 + 1) + 7\\ &= 9(333+55+8)+(3+5+8+7)\end{align*}
Geschiedenis van de negenproef
In de Griekse wiskunde komt de rest bij deling door 9 wel ter sprake, maar niet de eigenlijke negenproef. Die is ofwel een Arabische uitvinding, ofwel hebben de Arabische wiskundigen die geleerd van de Indiërs. In elk geval komt de negenproef voor in een werk van Al-Khwārizmī (9de eeuw). Hij legt in woorden uit hoe je de negenproef moet uitvoeren. Hij eindigt zijn uitleg met “en als het niet hetzelfde is, weet dan dat je je vergist hebt”. Bij andere Arabische auteurs kom je ook de zevenproef en de elfproef tegen.
De negenproef kwam in het begin van de 13de eeuw naar het Westen dank zij Leonardo van Pisa (Fibonacci). Niet alleen legt hij uit hoe je de negenproef moet uitvoeren, maar hij geeft ook een bewijs. Hij werkt hierbij met concrete getallen maar zijn redenering is algemeen. Ook Luca Pacioli (einde 15de eeuw) heeft het over de negenproef en de zevenproef, met een verwijzing naar Fibonacci. In figuur 1 zie je dat hij deze proeven ook toepast op een som. Onderaan lees je “prova per nove” en “prova per sette” (negenproef en zevenproef) met telkens de rest die je uitkomt (8 respectievelijk 4). Om een grotere zekerheid te hebben, past hij blijkbaar beide proeven toe; het zou al heel toevallig zijn dat een fout zowel de rest bij deling door negen als de rest bij deling door zeven ongemoeid laat…

Figuur 1 Berekening van Luca Pacioli





 Onder de loep
Onder de loep

