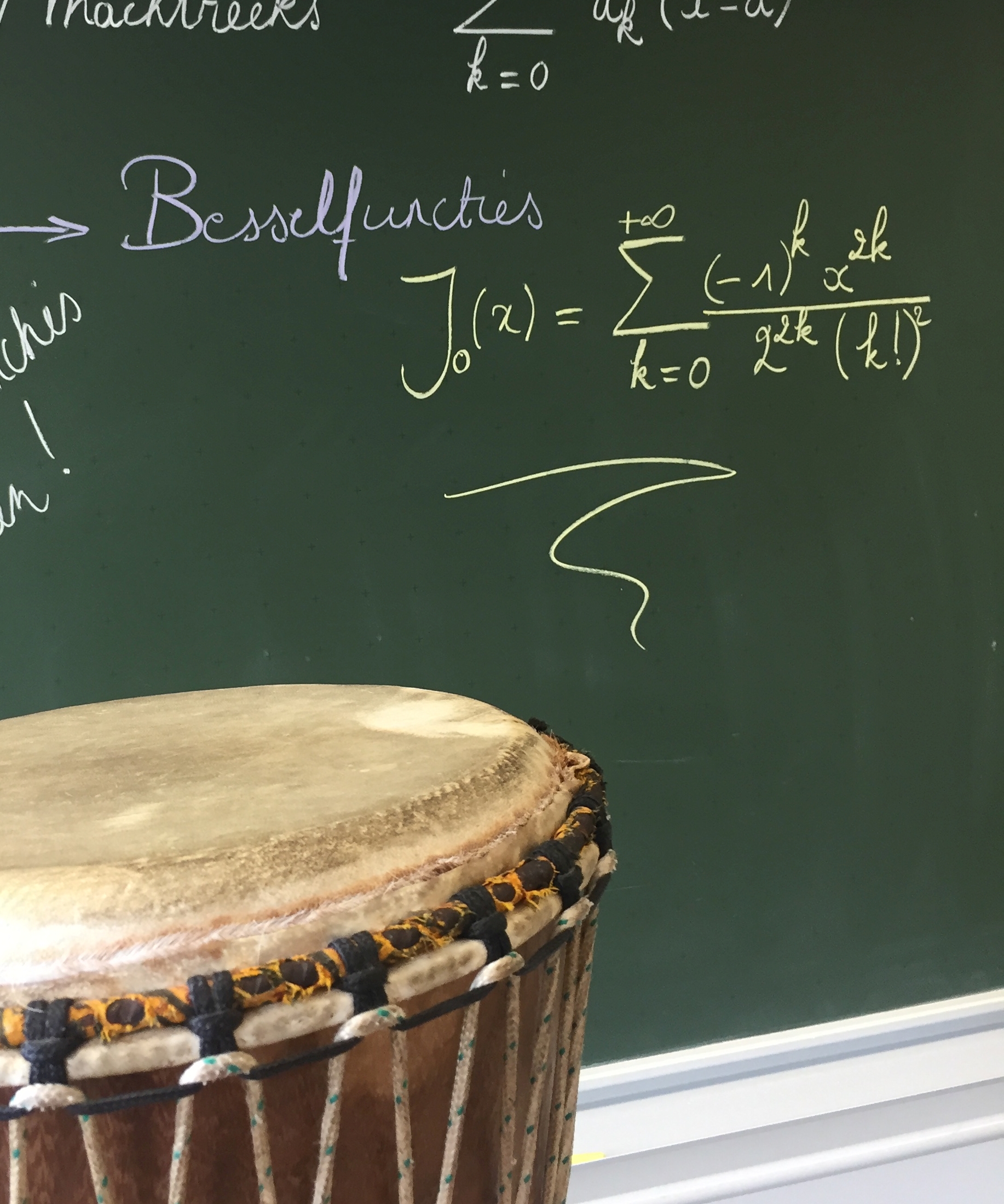Inloggen

Nummers & jaargangen

Uitwiskeling - Jaargang 33 - 2017

Verschenen nummers

Jaaroverzicht

33/1 - Verrijkende activiteiten in de eerste graad

De eerste graad is voor de leerlingen wennen aan een nieuwe wereld. De leerlingen komen uit verschillende lagere scholen en het niveau, zowel voor taal als voor wiskunde, is soms heel uiteenlopend. Daarom is het voor veel leerlingen nodig dat een deel van de leerstof van de lagere school wordt hernomen, terwijl anderen vooral uitkijken naar het 'nieuwe' dat ze op de grote school komen leren. Veel leerkrachten van de eerste graad zijn op zoek gegaan naar verrijkende activiteiten om al hun leerlingen de boeiende wereld van de wiskunde en haar toepassingen te laten ontdekken. In deze loep laten we enkele van deze collega’s aan het woord. (pg. 21))

  • Hilde Eggermont, Luc Van den Broeck, Michel Roelens en Gilberte Verbeeck
[ Lees meer ]
 

33/2 - Tensegrities

Tensegrities zijn een soort ruimtelijke constructies met staafjes en touwtjes die elkaar door trek- en spankrachten in evenwicht houden. In deze loep behandelen we bepaalde klassen van tensegrities die eenvoudig wiskundig kunnen worden nagerekend. Naast heel wat ruimtelijk inzicht volstaat hiervoor de wiskunde uit het vierde jaar. Met behulp van een 3D- designprogramma kunnen leerlingen daarna ook creatief aan de slag en hun eigen ontwerp maken. Als kers op de taart kunnen ze deze objecten tot slot nog knutselen. (pg. 18))

  • Luc Van den Broeck en Els Vanlommel
[ Lees meer ]
 

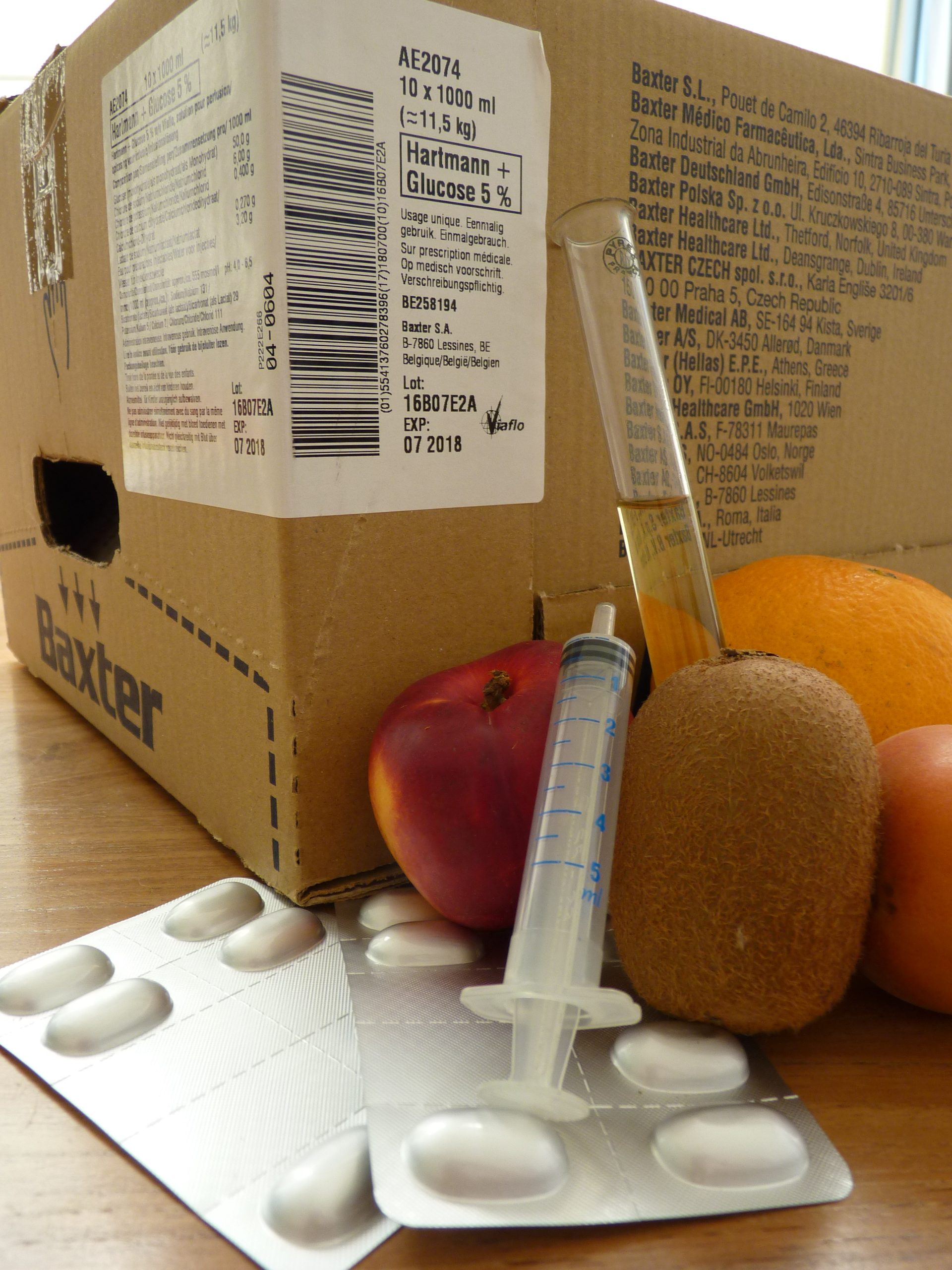
33/3 - Wiskunde en gezondheid

We richten ons op toepassingen van wiskunde in de medische wereld. Voor de A- en B-stroom in de eerste graad werkten we activiteiten uit die kaderen in een themaweek rond gezonde voeding en rond genotsmiddelen. Verder presenteren we materiaal over farmaceutisch rekenen, voor leerlingen van het vijfde jaar tso met 2 uur wiskunde per week en bruikbaar bij het leerplanonderdeel mathematiseren. Voor richtingen uit de derde graad met minimaal 4 u wiskunde per week werkten we toepassingen over exponentiële functies en rijen uit in de context van de farmacokinetiek: hoe evolueert de concentratie van een geneesmiddel in het lichaam? (pg. ))

  • Johan Deprez en Gerd Hautekiet
[ Lees meer ]
 

33/4 - Veeltermbenaderingen en machtreeksen

Veeltermfuncties worden vaak gebruikt om ‘moeilijkere’ functies te benaderen. Door ervoor te zorgen dat in een punt de opeenvolgende afgeleiden tot een bepaalde graad van de veeltermfunctie en de gegeven functie gelijk zijn, ontstaat een Taylorveelterm. Met GeoGebra kunnen leerlingen de grafiek van de functie vergelijken met die van zijn Taylorveeltermbenaderingen. We bewijzen een afschatting voor de ‘fout’ bij het vervangen van de functie door zo’n benadering. Een volgende stap is het werken met een ‘machtreeks’, een soort oneindige veelterm die in een bepaald gebied naar de functie kan convergeren. Dit levert een nieuwe bril op om de functie te bestuderen en zelfs te veralgemenen tot een complexe functie. We besteden aandacht aan de geschiedenis van deze veeltermen en machtreeksen alsook aan hun nut in de fysica en in de wiskunde. Een geschikt onderwerp voor leerlingen van het laatste jaar met minstens 6 wekelijkse lesuren wiskunde... (pg. 19))

  • Els Vanlommel en Michel Roelens
[ Lees meer ]
 
Bespreking van